题目内容
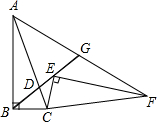 如图,在Rt△ABC中,∠B=90°,sin∠BAC=
如图,在Rt△ABC中,∠B=90°,sin∠BAC=| 1 |
| 3 |
考点:旋转的性质
专题:计算题
分析:作BH⊥CD于H,如图,在Rt△ABC中利用∠BAC的正弦可计算出AC=6,由于BC=BD=2,根据等腰三角形的性质得CH=DH,根据等角的余角相等得∠HBC=∠BAC,接着在Rt△HBC中利用sin∠HBC的正弦可计算出HC=
BC=
,则CD=2CH=
,所以AD=AC-CD=
,然后根据旋转的性质的∠BCE=∠ACF,CB=CE,CA=CF,根据两等腰三角形的两顶角相等,则底角相等得到∠CBE=∠CAF,易得∠AGD=∠BCD,再利用∠BCD=∠BDC可得∠ADG=∠AGD,于是根据等腰三角形的性质可得AG=AD=
.
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 14 |
| 3 |
| 14 |
| 3 |
解答:解: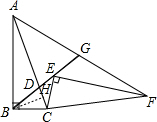 作BH⊥CD于H,如图,
作BH⊥CD于H,如图,
在Rt△ABC中,∠ABC=90°,∵sin∠BAC=
=
,
∴AC=3BC=6,
∵BC=BD=2,
∴CH=DH,
∵∠HBC+∠ACB=90°,∠BAC+∠ACB=90°,
∴∠HBC=∠BAC,
∴sin∠HBC=
,
在Rt△HBC中,∵sin∠HBC=
=
,
∴HC=
BC=
,
∴CD=2CH=
,
∴AD=AC-CD=6-
=
,
∵Rt△ABC绕点C旋转到Rt△FEC的位置,
∴∠BCE=∠ACF,CB=CE,CA=CF,
∴∠CBE=
(180°-∠BCE),∠CAF=
(180°-∠ACE),
∴∠CBE=∠CAF,
∵∠BDC=∠ADG,
∴∠AGD=∠BCD,
∵BC=BD,
∴∠BCD=∠BDC,
∴∠ADG=∠AGD,
∴AG=AD=
.
故答案为
.
 作BH⊥CD于H,如图,
作BH⊥CD于H,如图,在Rt△ABC中,∠ABC=90°,∵sin∠BAC=
| BC |
| AC |
| 1 |
| 3 |
∴AC=3BC=6,
∵BC=BD=2,
∴CH=DH,
∵∠HBC+∠ACB=90°,∠BAC+∠ACB=90°,
∴∠HBC=∠BAC,
∴sin∠HBC=
| 1 |
| 3 |
在Rt△HBC中,∵sin∠HBC=
| HC |
| BC |
| 1 |
| 3 |
∴HC=
| 1 |
| 3 |
| 2 |
| 3 |
∴CD=2CH=
| 4 |
| 3 |
∴AD=AC-CD=6-
| 4 |
| 3 |
| 14 |
| 3 |
∵Rt△ABC绕点C旋转到Rt△FEC的位置,
∴∠BCE=∠ACF,CB=CE,CA=CF,
∴∠CBE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CBE=∠CAF,
∵∠BDC=∠ADG,
∴∠AGD=∠BCD,
∵BC=BD,
∴∠BCD=∠BDC,
∴∠ADG=∠AGD,
∴AG=AD=
| 14 |
| 3 |
故答案为
| 14 |
| 3 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的性质和解直角三角形.

练习册系列答案
相关题目
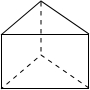 用平面去截如图所示的三棱柱,截面形状不可能是( )
用平面去截如图所示的三棱柱,截面形状不可能是( )| A、三角形 | B、四边形 |
| C、五边形 | D、六边形 |
下列图形中,必是相似形的是( )
| A、都有一个角是40°的两个等腰三角形 |
| B、都有一个角为50°的两个等腰梯形 |
| C、都有一个角是30°的两个菱形 |
| D、邻边之比为2:3的两个平行四边形 |
在数轴上,与表示数-5的点的距离是2的点表示的数是( )
| A、-3 | B、-7 |
| C、±3 | D、-3或-7 |
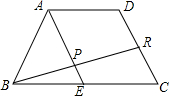 如图,B是平行四边形AECD边CE延长线上一点,且EB=EC,R为CD的中点,BR交AE于点P,则EP:AP=( )
如图,B是平行四边形AECD边CE延长线上一点,且EB=EC,R为CD的中点,BR交AE于点P,则EP:AP=( )A、
| ||
B、
| ||
C、
| ||
D、
|
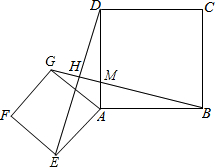 如图,点E是正方形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个正方形AEFG,线段GB与线段ED,AD分别交于点H,M.
如图,点E是正方形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个正方形AEFG,线段GB与线段ED,AD分别交于点H,M.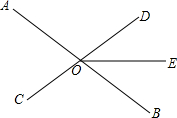 如图,直线AB、CD相交于点O,射线OE平分∠BOD.
如图,直线AB、CD相交于点O,射线OE平分∠BOD. 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3.