题目内容
13.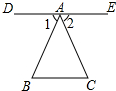 如图,有下列三个条件:①DE∥BC;②∠1=∠2;③∠B=∠C.
如图,有下列三个条件:①DE∥BC;②∠1=∠2;③∠B=∠C.(1)若从这三个条件中任选两个作为题设,另一个作为结论,组成一个命题,一共能组成几个命题,请你都写出来;
(2)你所写出的命题都是真命题吗?若是,请你就其中的一个真命题给出推理过程;若不是,请你对其中的假命题举出一个反例.(温馨提示:∠B+∠C+∠BAC=180°)
分析 (1)根据两条件一结论组成命题,可得答案;
(2)根据平行线的性质,可判定①②,根据平行线的判定,可判定③.
解答 解:(1)一共能组成三个命题,
如:①如果DE∥BC,∠1=∠2,那么∠B=∠C;
②如果DE∥BC,∠B=∠C,那么∠1=∠2;
③如果∠1=∠2,∠B=∠C,那么DE∥BC;
(2)都是真命题,
如果DE∥BC,∠1=∠2,那么∠B=∠C,
证明:∵DE∥BC,
∴∠1=B,∠2=∠C.
∵∠1=∠2,
∴∠B=∠C.
点评 本题考查了平行线的判定与性质,(1)利用了命题的定义,(2)利用了真命题的定义,平行线的判定与性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.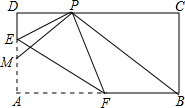 如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为( )
如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为( )
 如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为( )
如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为( )| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{9}$ |
2.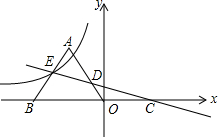 如图,△OAB为等腰直角三角形,斜边OB边在x负半轴上,一次函数y=-$\frac{1}{7}$x+$\frac{4}{7}$与△OAB交于E、D两点,与x轴交于C点,反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支过E点,若S△AED=S△DOC,则k的值为( )
如图,△OAB为等腰直角三角形,斜边OB边在x负半轴上,一次函数y=-$\frac{1}{7}$x+$\frac{4}{7}$与△OAB交于E、D两点,与x轴交于C点,反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支过E点,若S△AED=S△DOC,则k的值为( )
 如图,△OAB为等腰直角三角形,斜边OB边在x负半轴上,一次函数y=-$\frac{1}{7}$x+$\frac{4}{7}$与△OAB交于E、D两点,与x轴交于C点,反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支过E点,若S△AED=S△DOC,则k的值为( )
如图,△OAB为等腰直角三角形,斜边OB边在x负半轴上,一次函数y=-$\frac{1}{7}$x+$\frac{4}{7}$与△OAB交于E、D两点,与x轴交于C点,反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支过E点,若S△AED=S△DOC,则k的值为( )| A. | -$\frac{6}{7}$ | B. | -$\sqrt{3}$ | C. | -3 | D. | -4 |
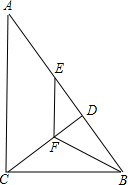 如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,点E在边AB上,且BE=BC,过点E作EF∥AC,交CD于F点,连接BF.
如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,点E在边AB上,且BE=BC,过点E作EF∥AC,交CD于F点,连接BF.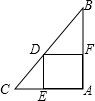 如图,正方形DEAF内接于△ABC,已知AC=8,AB=16,那么正方形的边长是$\frac{16}{3}$.
如图,正方形DEAF内接于△ABC,已知AC=8,AB=16,那么正方形的边长是$\frac{16}{3}$.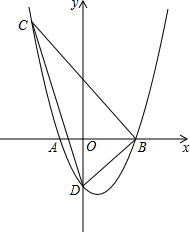 如图,抛物线经过A(-1,0),B(3,0),C(-2,5)三点,与y轴交于点D.
如图,抛物线经过A(-1,0),B(3,0),C(-2,5)三点,与y轴交于点D.
 计算下图阴影部分面积:
计算下图阴影部分面积: