题目内容
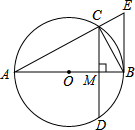 如图,AB为⊙O的直径,弦CD⊥AB于点M,过点B作BE∥CD,交AC的延长线于点E,连结BC.
如图,AB为⊙O的直径,弦CD⊥AB于点M,过点B作BE∥CD,交AC的延长线于点E,连结BC.(1)求证:BE为⊙O的切线;
(2)如果CD=6,BM:CM=1:2,求⊙O的直径.
考点:切线的判定
专题:
分析:(1)由BE∥CD,AB⊥CD,可证AB⊥BE,从而可证BE为⊙O的切线;
(2)由垂径定理知:CM=
CD,在Rt△BCM中,已知tan∠BCD和CM的值,可将BM,CM的值求出,由
=
,可知:∠BAC=∠BCD,在Rt△ACM中,根据三角函数可将AM的值求出,故⊙O的直径为AB=AM+BM.
(2)由垂径定理知:CM=
| 1 |
| 2 |
 |
| BC |
 |
| BD |
解答:解:(1)证明:∵BE∥CD,AB⊥CD,
∴AB⊥BE.
∵AB是⊙O的直径,
∴BE为⊙O的切线.
(2)解:∵AB是⊙O的直径,AB⊥CD,
∴CM=
CD,
=
,CM=
CD=3,
∴∠BAC=∠BCD.
∵BM:CM=1:2,
∴BM=
,
∵CM:AM=1:2.
∴AM=6.
∴AB=AM+BM=7.5.
∴AB⊥BE.
∵AB是⊙O的直径,
∴BE为⊙O的切线.
(2)解:∵AB是⊙O的直径,AB⊥CD,
∴CM=
| 1 |
| 2 |
 |
| BC |
 |
| BD |
| 1 |
| 2 |
∴∠BAC=∠BCD.
∵BM:CM=1:2,
∴BM=
| 3 |
| 2 |
∵CM:AM=1:2.
∴AM=6.
∴AB=AM+BM=7.5.
点评:此题考查了切线的判定,垂径定理,锐角三角函数定义,以及圆周角定理,熟练掌握切线的判定方法是解本题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
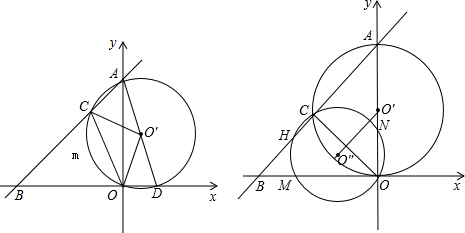
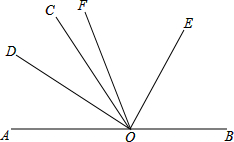 如图,点O为直线AB上一点,过点O作直线OC,已知∠AOC≠90°,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE.求:
如图,点O为直线AB上一点,过点O作直线OC,已知∠AOC≠90°,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE.求: 在由边长为1的小正方形组成的网格中,建立如图所示的平面直角坐标系.
在由边长为1的小正方形组成的网格中,建立如图所示的平面直角坐标系.