题目内容
18. 如图,在平面直角坐标系中,点C在y轴上,点A(a,0)、点B(a-4,0),位于原点两侧,且∠ABC=60°,AE⊥BC,交y轴于点F,交BC于点E,点D在点B的左侧,且∠CDO=45°,AB=2BD
如图,在平面直角坐标系中,点C在y轴上,点A(a,0)、点B(a-4,0),位于原点两侧,且∠ABC=60°,AE⊥BC,交y轴于点F,交BC于点E,点D在点B的左侧,且∠CDO=45°,AB=2BD(1)直接写出∠BCD的度数、AB的长及点C的纵坐标(用含有a的式子表示)
①∠BCD=15°
②AB=4
③C(0,6-a)
(2)求∠ACD的度数;
(3)求点F的坐标(用含有a的式子表示)
分析 (1)①在△BCD中利用三角形外角的性质可求得∠BCD;②利用A、B的坐标可求得AB的长;③由条件可求得OD的长度,则可求得OC的长,可求得C点纵坐标;
(2)连接DE,利用直角三角形的性质可求得BE=BD,进一步可求得DE=AE,可求得CE=AE,则可求得∠ACD;
(3)在Rt△OAF中可求得∠FAO,利用三角函数值可求得OF的长,则可求得F点的坐标.
解答 解:
(1)①∵∠CDO=45°,∠ABC=60°,
∴∠BCD=∠ABC-∠CDO=60°-45°=15°
故答案为:15°;
②∵A(a,0)、点B(a-4,0),
∴AB=a-(a-4)=4,
故答案为:4;
③∵AB=2BD,
∴BD=$\frac{1}{2}$AB=2,
∴AD=AB+BD=6,且OA=a,
∴OC=OD=6-a,
∴C(0,6-a),
故答案为:6-a;
(2)如图同,连接DE,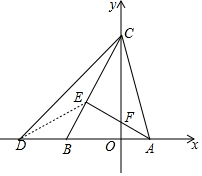
∵AE⊥BC,
∴∠AEB=∠CEF=90°,
∵∠ABC=60°,
∴∠BAE=90°-60°=30°,
在Rt△ABE中,BE=$\frac{1}{2}$AB,
∵AB=2BD,即BD=$\frac{1}{2}$AB,
∴BE=BD,
∴∠EDB=∠BED,
∵∠EDB+∠BED=∠ABC=60°,
∴∠EDB=30°,
∴∠CDE=∠CDO-∠EDB=15°,
∴∠CDE=∠BCD=15°,
∴DE=CE,
∵∠EDB=∠BAE=30°,
∴DE=AE,
∴CE=AE,
∴△ACE是等腰直角三角形,
∴∠ACE=45°,
∴∠ACD=∠ACE+∠BCD=45°+15°=60°;
(3)由(2)可知∠BAE=30°,且OA=a,
∴$\frac{OF}{OA}$=tan∠BAE,即$\frac{OF}{a}$=$\frac{\sqrt{3}}{3}$,
∴OF=$\frac{\sqrt{3}}{3}$a,
∴F(0,$\frac{\sqrt{3}}{3}$a).
点评 本题为三角形的综合应用,涉及三角形外角的性质、直角三角形的性质、等腰三角形的判定和性质及三角函数等知识.在(2)中构造三角形,证明△ACE为等腰直角三角形是解题的关键.本题考查知识点较多,综合性较强,难度适中.

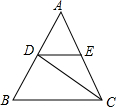 如图,△ABC中,AB=AC=BC,CD是∠ACB的平分线,过D作DE∥BC交AC于E,若△ABC的边长为a,则△ADE的周长是( )
如图,△ABC中,AB=AC=BC,CD是∠ACB的平分线,过D作DE∥BC交AC于E,若△ABC的边长为a,则△ADE的周长是( )| A. | 2a | B. | $\frac{4}{3}$a | C. | $\frac{3}{2}$a | D. | a |
| A. | $\frac{6}{7}$ | B. | -3 | C. | 3 | D. | 7 |

| A. | SSS | B. | SAS | C. | AAS | D. | ASA |
 在数轴上,把表示数1的点称为基准点,记作点$\stackrel{•}{O}$.对于两个不同的点M和N,若点M、点N到点$\stackrel{•}{O}$的距离相等,则称点M与点N互为基准变换点.例如:图1中,点M表示数-1,点N表示数3,它们与基准点$\stackrel{•}{O}$的距离都是2个单位长度,点M与点N互为基准变换点.
在数轴上,把表示数1的点称为基准点,记作点$\stackrel{•}{O}$.对于两个不同的点M和N,若点M、点N到点$\stackrel{•}{O}$的距离相等,则称点M与点N互为基准变换点.例如:图1中,点M表示数-1,点N表示数3,它们与基准点$\stackrel{•}{O}$的距离都是2个单位长度,点M与点N互为基准变换点.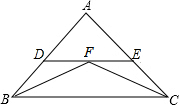 如图,已知DE∥BC,∠ABC和∠ACB的平分线交于DE上一点F,求证:DE=DB+EC.
如图,已知DE∥BC,∠ABC和∠ACB的平分线交于DE上一点F,求证:DE=DB+EC.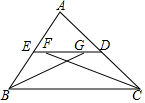 如图,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若FG=2,ED=6,则EB+DC=8.
如图,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若FG=2,ED=6,则EB+DC=8.