题目内容
13.已知关于x的一元二次方程x2+ax+b=0有一个非零根-b,则a-b的值为( )| A. | -1 | B. | 0 | C. | 1 | D. | -2 |
分析 由于关于x的一元二次方程x2+ax+b=0有一个非零根-b,那么代入方程中即可得到b2-ab+b=0,再将方程两边同时除以b即可求解.
解答 解:∵关于x的一元二次方程x2+ax+b=0有一个非零根-b,
∴b2-ab+b=0,
∵-b≠0,
∴b≠0,
方程两边同时除以b,得b-a+1=0,
∴a-b=1.
故选:C.
点评 此题主要考查了一元二次方程的解,解题的关键是把已知方程的根直接代入方程进而解决问题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
4.16的平方根是( )
| A. | ±4 | B. | ±$\sqrt{2}$ | C. | 2 | D. | ±2 |
1. 如图所示的图案绕旋转中心旋转一定角度后能够与自身重合,那么这个旋转角可能是( )
如图所示的图案绕旋转中心旋转一定角度后能够与自身重合,那么这个旋转角可能是( )
 如图所示的图案绕旋转中心旋转一定角度后能够与自身重合,那么这个旋转角可能是( )
如图所示的图案绕旋转中心旋转一定角度后能够与自身重合,那么这个旋转角可能是( )| A. | 60° | B. | 72° | C. | 90° | D. | 120° |
18.下列交通标志图形好是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
5.下列分解因式正确的是( )
| A. | a2-9=(a-3)2 | B. | -4a+a2=-a(4+a) | C. | a2+6a+9=(a+3)2 | D. | a2-2a+1=a(a-2)+1 |
3.如果一个角的补角比它的余角度数的3倍少10°,则这个角的度数是( )
| A. | 60° | B. | 50° | C. | 45° | D. | 40° |
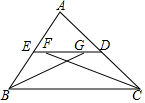 如图,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若FG=2,ED=6,则EB+DC=8.
如图,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若FG=2,ED=6,则EB+DC=8.