题目内容
2.节约1度电,可以减少0.785千克碳排放.某省从2011年6月1日起执行新的居民生活用电价格,一户一表居民用户将实施阶梯式累进电价:月用电量低于50千瓦时(含50千瓦时)部分不调整,电价每千瓦时0.53元;月用电量在51~200千瓦时部分,电价每千瓦时上调0.03元;月用电量超过200千瓦时部分,电价每千瓦时上调0.10元.小明家属一户一表居民用户,将实施阶梯式累进电价,7月份至8月份的电费缴款情况如下表:| 计算日期 | 上期示度 | 本期示度 | 电量 | 金额(元) |
| 20110710 | 3 230 | 3 296 | 66 | 34.98 |
| 20110810 | 3 296 | 3 535 | 239 | 135.07 |
(2)解释小明家8月份电费的计算详情.
(3)为节约用电,小明对以后制订了详细的用电计划,如果实际每天比计划多用2千瓦时,下月用电量将会超过240千瓦时;如果实际每天比计划节约2千瓦时,那么下月用电量将会不超过180千瓦时,下月(30天)每天用电量应控制在什么范围内?
分析 (1)读懂题意,列式得出关系式,进而画出图象;
(2)读懂题意,进而解释小明家8月份电费的计算详情即可;
(3)设下月小明家的用电量是x千瓦时,根据题意求解即可.
解答 解:(1)当x≤50时,y=0.53x;
当51≤x≤200时,y=(0.53+0.03)x=0.56x;
当x>200时,y=(0.53+0.1)x=0.63x;
图象如图表示: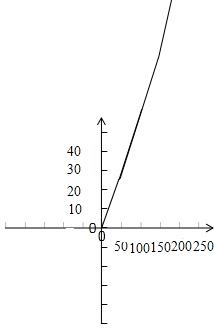
(2)因为239>200,所以小明家8月份电费是每千瓦时(0.53+0.1)=0.63元,故电费是239×0.63=135.07元;
(3)设下月小明家的用电量是x千瓦时,可得:$\left\{\begin{array}{l}{(\frac{x}{30}+2)×30>240}\\{(\frac{x}{30}-2)×30≤180}\end{array}\right.$,
可得:150<x≤240.
所以下月(30天)每天用电量应控制在5<x≤8.
点评 此题考查一次函数的应用,关键是根据电费的分阶段缴费得出关系式解答即可.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
10. 如图,DE∥BC,AD:DB=1:2,则△ADE和△ABC的相似比为( )
如图,DE∥BC,AD:DB=1:2,则△ADE和△ABC的相似比为( )
 如图,DE∥BC,AD:DB=1:2,则△ADE和△ABC的相似比为( )
如图,DE∥BC,AD:DB=1:2,则△ADE和△ABC的相似比为( )| A. | 1:2 | B. | 1:3 | C. | 2:1 | D. | 2:3 |
11.正六边形的边心距是$\sqrt{3}$,则它的边长是( )
| A. | 1 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
 甲从M地出发去N地,乙搭甲的便车也从M地出发到途中与M,N两地在同一条直线上的G地.甲在N地停留一段时间后以110km/h的速度返回,乙在G地停留了$\frac{3}{4}$h后,徒步返回M地,走了5km时与返回的甲相遇并搭甲车返回M地.如图是两人与M地的距离y(单位:km)与行进时间x(单位:h)之间的函数图象(甲、乙均匀速行进,不考虑其他因素).
甲从M地出发去N地,乙搭甲的便车也从M地出发到途中与M,N两地在同一条直线上的G地.甲在N地停留一段时间后以110km/h的速度返回,乙在G地停留了$\frac{3}{4}$h后,徒步返回M地,走了5km时与返回的甲相遇并搭甲车返回M地.如图是两人与M地的距离y(单位:km)与行进时间x(单位:h)之间的函数图象(甲、乙均匀速行进,不考虑其他因素).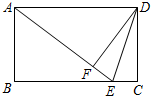 如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=3,BE:EC=4:1,则线段DE的长为$\sqrt{10}$.
如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=3,BE:EC=4:1,则线段DE的长为$\sqrt{10}$.