Question

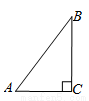
如图，在Rt△ABC中,∠C = 90°，BC=9,CA=12,∠ABC的平分线BD交AC于点D, DE⊥DB交AB于点E. 点O在AB上，⊙O是△BDE的外接圆,交BC于点F,连结EF.求的值.

Answer 1

【解析】

试题分析：首先根据BC和AC的长度求出AB的长度，根据平分线的性质得出∠ABD=∠DBC，根据OB=OD得出∠ABD=∠ODB，从而说明∠ODB=∠DBC，得到OD∥BC，从而说明△ADO和△ACB相似，求出圆的半径，然后证明出△BEF和△BAC相似，求出所求的结果.

试题解析：连接OD，设⊙O的半径为r, 在Rt△ABC中, ,

∴AB=15 ∵BD平分∠ABC， ∴∠ABD=∠DBC ∵OB=OD ∴∠ABD=∠ODB ∴∠ODB=∠DBC

∴OD//BC ∴∠ADO=∠C=90° 又∠A=∠A ∴△ADO∽△ACB

∴. ∴ ∴. ∴

又∵BE是⊙O的直径. ∴∠BFE=90° ∴△BEF∽△BAC ∴

考点：三角形相似的应用.