题目内容
1.判断下列说法是否正确,并简要说明理由.(1)如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形;
(2)等腰三角形两腰上的中线相等;
(3)平行于等腰三角形一边的直线所截得的三角形仍是等腰三角形.
分析 (1)可依据题意先作出简单的图形,结合图形可得∠B=∠A,进而可得其为等腰三角形;
(2)先根据题意作图,结合图形写出已知,求证,然后再根据已知和图形进行证明.可根据等腰三角形的性质得出相关的等角或相等的线段:DC=BE,∠DCB=∠EBC,BC=CB,可证明△BDC≌△CEB,所以BD=CE,即等腰三角形的两腰上的中线相等;
(3)首先根据题意画出图形,由AB=AC,DE∥BC,即可得到结论.
解答 解: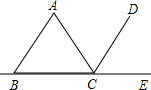 (1)如图,
(1)如图,
DC平分∠ACE,且AB∥CD,
∴∠ACD=∠DCE,∠A=∠ACD,∠B=∠DCE
∴∠B=∠A,
∴△ABC为等腰三角形;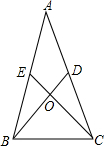 (2)已知:等腰△ABC中,AB=AC,AD=DC,AE=EB,
(2)已知:等腰△ABC中,AB=AC,AD=DC,AE=EB,
求证:BD=CE.
证明:∵AB=AC,AD=DC,AE=EB,
∴DC=BE,∠DCB=∠EBC.
∵BC=CB,
∴△BDC≌△CEB(SAS).
∴BD=CE.
即等腰三角形的两腰上的中线相等;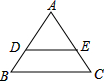 (3)如图,根据题意得:AB=AC,DE∥BC,
(3)如图,根据题意得:AB=AC,DE∥BC,
∴∠B=∠C,∠ADE=∠B,∠ADE=∠C,
∴∠ADE=∠AED,
∴△ADE是等腰三角形.
点评 本题考查的是等腰三角形的判定和性质,三角形的外角及平行线的性质,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
9.下列运算中正确的是( )
| A. | 4a-3a=1 | B. | a•a2=a3 | C. | (a-b)2=a2-b2 | D. | (2ab2)3=6a3b6 |
 如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连结AC并延长到D,使CD=CA.连结BC并延长到E,使EC=CB,连结DE,量出DE的长,就是A、B的距离.写出你的证明.
如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连结AC并延长到D,使CD=CA.连结BC并延长到E,使EC=CB,连结DE,量出DE的长,就是A、B的距离.写出你的证明. 已知二次函数y=-x2+4x+5,完成下列各题:
已知二次函数y=-x2+4x+5,完成下列各题: