题目内容
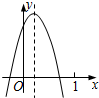 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①abc>0;②方程x2+bx+c=0的两根之和大于0;③y随x的增大而增大;④a-b+c<0,
其中正确的个数( )
| A、4个 | B、3个 | C、2个 | D、1个 |
考点:二次函数图象与系数的关系
专题:数形结合
分析:由抛物线开口方向得a<0,由抛物线的对称轴在y轴的右侧得到-
>0,则b>0,由抛物线与x轴的交点在x轴上方得c>0,所以abc<0,于是可对①进行判断;根据根与系数的关系得到方程x2+bx+c=0的两根之和等于-
,利用ab<0可对②进行判断;根据二次函数的性质对③进行判断;根据抛物线的对称性得到抛物线与x轴的另一个交点在点(0,0)和(-1,0)之间,则x=-1时,y<0,即a-b+c<0,于是可对④进行判断.
| b |
| 2a |
| b |
| a |
解答:解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴在y轴的右侧,
∴x=-
>0,
∴b>0,
∵抛物线与x轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①错误;
∵方程x2+bx+c=0的两根之和等于-
,
而ab<0,
∴程x2+bx+c=0的两根之和大于0,所以②正确;
∵当x<-
时,y随x的增大而增大,所以③错误;
∵抛物线与x轴的一个交点在点(0,0)和(1,0)之间,
而对称轴在y轴的右侧,
∴抛物线与x轴的另一个交点在点(0,0)和(-1,0)之间,
∴x=-1时,y<0,即a-b+c<0,所以④正确.
故选C.
∴a<0,
∵抛物线的对称轴在y轴的右侧,
∴x=-
| b |
| 2a |
∴b>0,
∵抛物线与x轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①错误;
∵方程x2+bx+c=0的两根之和等于-
| b |
| a |
而ab<0,
∴程x2+bx+c=0的两根之和大于0,所以②正确;
∵当x<-
| b |
| 2a |
∵抛物线与x轴的一个交点在点(0,0)和(1,0)之间,
而对称轴在y轴的右侧,
∴抛物线与x轴的另一个交点在点(0,0)和(-1,0)之间,
∴x=-1时,y<0,即a-b+c<0,所以④正确.
故选C.
点评:本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定,△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )A、 |
B、 |
C、 |
D、 |
截止到4月25日,雅安三个重灾县的直接经济损失已经达到了上年GDP总和的21倍,已知上年GDP总和约为80亿元,则三个重灾县的直接经济损失用科学记数法表示约为( )
| A、1680亿元 |
| B、1.68×1011元 |
| C、1.68×1012元 |
| D、0.168×1012元 |
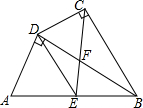 如图,四边形ABCD中,∠ADB=∠DCB=90°,BD平分∠ABC,点E为AB中点.
如图,四边形ABCD中,∠ADB=∠DCB=90°,BD平分∠ABC,点E为AB中点. 二次函数y=ax2+bx+c的图象如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,求k的取值范围.
二次函数y=ax2+bx+c的图象如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,求k的取值范围. 已知,如图,AB=AC,BD平分∠ABC,CD平分∠ACB.求证:AD⊥BC.
已知,如图,AB=AC,BD平分∠ABC,CD平分∠ACB.求证:AD⊥BC.