题目内容
8.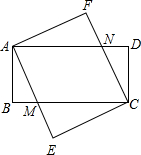 已知:如图,四边形ABCD和四边形AECF都是矩形,AE与BC交于点M,CF与AD交于点N.
已知:如图,四边形ABCD和四边形AECF都是矩形,AE与BC交于点M,CF与AD交于点N.(1)求证:△ABM≌△CDN;
(2)矩形ABCD和矩形AECF满足何种关系时,四边形AMCN是菱形,证明你的结论.
分析 (1)利用矩形的性质结合平行四边形的判定于性质得出AM=CN,进而得出Rt△ABM≌Rt△CDN;
(2)利用全等三角形的判定得出△ABM≌△AFN(ASA),进而得出四边形AMCN是菱形.
解答  (1)证明:∵四边形ABCD是矩形,
(1)证明:∵四边形ABCD是矩形,
∴∠B=∠D=90°,AB=CD,AD∥BC,
∵四边形AECF是矩形,∴AE∥CF,
∴四边形AMCN是平行四边形,
∴AM=CN,
在Rt△ABM和Rt△CDN中,
∵$\left\{\begin{array}{l}{AB=CD}\\{AM=CN}\end{array}\right.$,
∴Rt△ABM≌Rt△CDN(HL);
(2)解:当AB=AF时,四边形AMCN是菱形,
理由:∵四边形ABCD、AECF是矩形,
∴∠B=∠BAD=∠EAF=∠F=90°,
∴∠BAD-∠NAM=∠EAF-∠NAM,即∠BAM=∠FAN,
在△ABM和△AFN中∠BAM=∠FAN,AB=AF,∠B=∠F
∵$\left\{\begin{array}{l}{∠BAM=∠FAN}\\{AB=AF}\\{∠B=∠F}\end{array}\right.$,
∴△ABM≌△AFN(ASA),
∴AM=AN,
由(1)知四边形AMCN是平行四边形,
∴平行四边形AMCN是菱形.
点评 此题主要考查了菱形的判定以及全等三角形的判定与性质,熟练应用全等三角形的判定与性质是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列计算正确的是( )
| A. | x6÷x2=x3 | B. | $3{m^{-2}}=\frac{1}{{3{m^2}}}$ | C. | (a3b)2=a6b2 | D. | (a2)4=a6 |
3.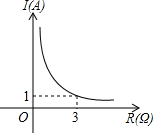 某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图所示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为( )
某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图所示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为( )
 某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图所示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为( )
某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图所示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为( )| A. | $I=\frac{2}{R}$ | B. | $I=\frac{3}{R}$ | C. | $I=\frac{5}{R}$ | D. | $I=\frac{6}{R}$ |
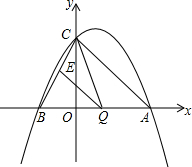 如图,已知抛物线与y轴交于点C(0,4),与x轴交于A(x1,0)、B(x2,0),其中x1,x2为方程x2-2x-8=0的两个根.
如图,已知抛物线与y轴交于点C(0,4),与x轴交于A(x1,0)、B(x2,0),其中x1,x2为方程x2-2x-8=0的两个根.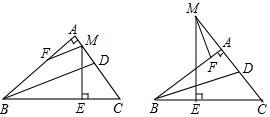
 在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点,且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点…则边长为8的正方形内部的整点的个数为( )
在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点,且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点…则边长为8的正方形内部的整点的个数为( )