题目内容
17．在数轴上A、B两点表示的数分别是-$\sqrt{2}$、$\sqrt{7}$，则A、B两点间表示整数的点有4个．分析 先估算出$\sqrt{2}$和$\sqrt{7}$的值，再根据范围求出即可．
解答 解：∵1＜$\sqrt{2}$＜2，2$＜\sqrt{7}$＜3，
∴-2＜-$\sqrt{2}$＜-1，
∵在数轴上A、B两点表示的数分别是-$\sqrt{2}$、$\sqrt{7}$，
∴A、B两点间表示整数的点有-1，0，1，2，共4个．
故答案为：4．
点评 本题考查了估算无理数的大小，实数的大小比较的应用，能估算出-$\sqrt{2}$和$\sqrt{7}$的范围是解此题的关键．
练习册系列答案
相关题目
8．已知命题“若a=b，则a2=b2”，则该命题的逆命题为（ ）
| A． | 若a≠b，则a2=b2 | B． | 若a2=b2，则a≠b | C． | 若a=b，则a2≠b2 | D． | 若a2=b2，则a=b |
12．下列各数中是无理数的是（ ）
| A． | $\sqrt{2}$ | B． | 3.14 | C． | $\root{3}{8}$ | D． | $\frac{1}{3}$ |
如图，四边形ABCD中，AB=3cm，AD=4cm，BC=13cm，CD=12cm，∠A=90°，求四边形ABCD的面积．
9．若关于x的方程（a-1）x2+2x-1=0是一元二次方程，则a的取值范围是（ ）
| A． | a≠1 | B． | a＞1 | C． | a＜1 | D． | a≠0 |
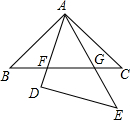如图，△ABC与△DEA是两个全等的等腰直角三角形，∠BAC=∠D=90°，△DEA绕点A旋转，边AD、AE与BC分别与AD、AE相交于点F、G，CB=5．回答下列问题．