题目内容
新定义:[a,b]为一次函数y=ax+b(a≠0,a,b为实数)的“关联数”.若“关联数”[2,m+1]的一次函数是正比例函数,则关于x的方程
+
=1的解为 .
| 1 |
| x-1 |
| 1 |
| m |
考点:解分式方程,正比例函数的定义
专题:新定义
分析:根据题中的新定义化简求出m的值,代入分式方程计算即可求出解.
解答:解:根据关联数”[2,m+1]的一次函数是正比例函数,得到m+1=0,即m=-1,
则方程为
-1=1,即x-1=
,
解得:x=
,
经检验是分式方程的解.
故答案为:
则方程为
| 1 |
| x-1 |
| 1 |
| 2 |
解得:x=
| 3 |
| 2 |
经检验是分式方程的解.
故答案为:
| 3 |
| 2 |
点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
不等式
<1的正整数解为( )
| 4x-5 |
| 11 |
| A、1个 | B、3个 | C、4个 | D、5个 |

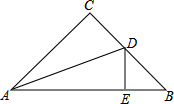 如图,在等腰直角△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于E,若AC=6,则△BDE的周长等于
如图,在等腰直角△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于E,若AC=6,则△BDE的周长等于 一次函数y=kx+b的图象如图,看图填空:
一次函数y=kx+b的图象如图,看图填空: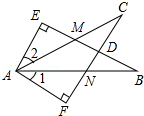 如图∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:
如图∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论: