题目内容
在我们生活中通常用两种方法来确定物体的位置．如小岛A在码头O的南偏东60°方向的14千米处，若以码头O为坐标原点，正东方向为x轴的正方向，正北方向为y轴的正方向，1千米为单位长度建立平面直角坐标系，则小岛A也可表示成____________
（7，-7）
【解析】试题分析：过点A作AC⊥x轴于C，
在Rt△OAC中，∠AOC=90°-60°=30°，OA=14千米， 则AC=7千米，OC=7千米，
因而小岛A所在位置的坐标是（7，-7）．
中考解读考点精练系列答案已知抛物线的顶点坐标为P（2，-1），它的图象经过点C（0，3）．
（1）求该抛物线的解析式．
（2）设该抛物线的图象与x轴交于A、B两点，求△ABC的面积．
（1）；（2）3
【解析】分析：（1）设该抛物线方程为 ，然后将点（3，0）代入求得k的值；（2）令y=0，求出抛物线与x轴的交点坐标，然后根据三角形的面积公式列式计算求解．
本题解析：（1）∵抛物线的顶点坐标为P（2，-1），
∴设该抛物线方程为，（k≠0）；
∵它的图象经过点C（0，3），
∴，
解得k=1，
∴该抛物线的解析式为，即；
（2）令... 分式方程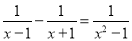
去分母时，两边都乘以________.
(x+1)(x-1))
【解析】∵分式方程 可化为： ，
∴去分母时，方程两边应都乘以： . 平时我们在跳绳时，绳摇到最高点处的形状可近似地看做抛物线，如图所示．正在摇绳的甲、乙两名同学拿绳的手间距为4 m，距地高均为1 m，学生丙、丁分别站在距甲拿绳的手水平距离1 m，2．5 m处．绳子在摇到最高处时刚好通过他们的头顶．已知学生丙的身高是1．5 m，则学生丁的身高为 ( )
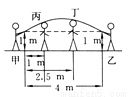
A. 1.5 m B. 1.625 m C. 1.66 m D. 1.67 m
B
【解析】设所求的函数的解析式为y=ax2+bx+c，由已知，函数的图象过（-1，1），（0，1.5），（3，1）三点，易求其解析式为y=-x2+x+,∵丁头顶的横坐标为1.5，∴代入其解析式可求得其纵坐标为1.625m.故选B. 如图，某渔船在海面上朝正西方向以20海里/时匀速航行，在A处观测到灯塔C在北偏西60°方向上，航行1小时到达B处，此时观察到灯塔C在北偏西30°方向上，若该船继续向西航行至离灯塔距离最近的位置，求此时渔船到灯塔的距离（结果精确到1海里，参考数据：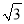 
≈1.732）
17．
【解析】试题分析：过点C作CD⊥AB于点D，则若该船继续向西航行至离灯塔距离最近的位置为CD的长度，利用锐角三角函数关系进行求解即可．
试题解析：如图，过点C作CD⊥AB于点D，
AB=20×1=20（海里），∵∠CAF=60°，∠CBE=30°，∴∠CBA=∠CBE+∠EBA=120°，∠CAB=90°﹣∠CAF=30°，∴∠C=180°﹣∠CBA﹣∠CAB=30°，∴... 如图，小明同学在东西方向的环海路A处，测得海中灯塔P在北偏东60°方向上，在A处东500米的B处，测得海中灯塔P在北偏东30°方向上，则灯塔P到环海路的距离PC=（ ）米．
A. 250 B. 500 C. 250
D. 500
C
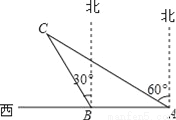
【解析】试题分析：设PC=x米，根据Rt△PBC的性质可得：BC=x米，根据Rt△PAC的性质可得：AC=x米，AB=AC-BC=x-x=500，解得：x=250米，故选C． 如图，杭州市郊外一景区内有一条笔直的公路a经过两个景点A，B，景区管委会又开发了风景优美的景点C，经测量景点C位于景点A的北偏东60°方向，又位于景点B的北偏东30°方向，且景点A、B相距200m，则景点B、C相距的路程为（ ）
A. 100
B. 200 C. 100 D. 200
B
【解析】试题分析：根据方位角可得：∠A=30°，∠CBA=120°，则∠C=30°，则△ABC为等腰三角形，故BC=AB=200m，故选B． 平行四边形的一条边长是12cm，那么它的两条对角线的长可能是（ ）
A. 8cm和16cm B. 10cm和16cm C. 8cm和14cm D. 8cm和12cm
B
【解析】试题解析：对于A，两条对角线的一半长分别为4cm，8cm，由于4+8=12，故不能构成三角形，故A不符合题意；
对于B，两条对角线的一半长分别为5cm，8cm，由于5+8＞12，故能构成三角形，故B符合题意；
对于C，两条对角线的一半长分别为4cm，7cm，由于4+7＜12，故不能构成三角形，故C不符合题意；
对于D，两条对角线的一半长分别为4cm，6cm，由于... 为改善环境，张村拟在荒山上种植960棵树，由于共青团员的支持，每日比原计划多种20棵，结果提前4天完成任务，原计划每天种植多少棵？设原计划每天种植x棵，根据题意得方程______________.
【解析】设原计划每天种植x棵，根据题意：
故答案： .