题目内容
19.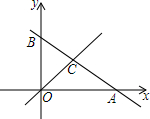 如图,直线y1=-$\frac{1}{2}$x+2与x轴、y轴分别交于点A和点B,直线y2过原点O且与直线
如图,直线y1=-$\frac{1}{2}$x+2与x轴、y轴分别交于点A和点B,直线y2过原点O且与直线y1=-$\frac{1}{2}$x+2交于点$C({\frac{4}{3},a})$.
(1)求点A和点B坐标;
(2)求出直线y2的解析式;
(3)根据图象可知:当x<$\frac{4}{3}$时,y1>y2,y1=-$\frac{1}{2}$x+2.
分析 (1)由直线y1=-$\frac{1}{2}$x+2,令y=0,则-$\frac{1}{2}$x+2=0,解得x=4,令x=0,则y=2,从而求得A、B的坐标;
(2)把点$C({\frac{4}{3},a})$代入y1=-$\frac{1}{2}$x+2求得a的值,然后根据待定系数法即可求得;
(3)根据图象,结合解得坐标即可求得.
解答 解:(1)∵直线y1=-$\frac{1}{2}$x+2与x轴、y轴分别交于点A和点B,
∴令y=0,则-$\frac{1}{2}$x+2=0,解得x=4,
令x=0,则y=2,
∴A(4,0),B(0,2);
(2)∵直线y1=-$\frac{1}{2}$x+2与直线y2交于点$C({\frac{4}{3},a})$.
∴a=-$\frac{1}{2}$×$\frac{4}{3}$+2=$\frac{4}{3}$,
∴C($\frac{4}{3}$,$\frac{4}{3}$),
设直线y2过的解析式为y2=kx,
∴$\frac{4}{3}$k=$\frac{4}{3}$,
∴k=1,
∴直线y2的解析式为y2=x;
(3)根据图象可知:当x<$\frac{4}{3}$时,y1>y2.
故答案为<$\frac{4}{3}$.
点评 本题考查了两条直线相交或平行问题:两条直线的交点坐标,符合这两条直线相对应的一次函数表达式.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
9.下面是四组线段的长度,哪一组能组成三角形( )
| A. | 2,2,4 | B. | 5,5,5 | C. | 11,5,6 | D. | 3,8,24 |
11.抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x,纵坐标y的对应值如表:
从上表可知,下列说法错误的是( )
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | -$\frac{3}{2}$ | 1 | $\frac{5}{2}$ | 3 | $\frac{5}{2}$ | 1 | … |
| A. | 对称轴为直线x=2 | B. | 图象开口向下 | C. | 顶点坐标(2,3) | D. | 当x=5时,y=$\frac{3}{2}$ |
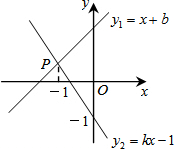 如图,已知直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b≤kx-1的解集在数轴上表示正确的是( )
如图,已知直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b≤kx-1的解集在数轴上表示正确的是( )
 已知,直线y=2x+4与直线y=-2x-2.
已知,直线y=2x+4与直线y=-2x-2.
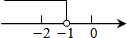
 有理数a、b、c在数轴上的位置如图所示,试化简:|c-b|-|a-b|+|c|.
有理数a、b、c在数轴上的位置如图所示,试化简:|c-b|-|a-b|+|c|.