题目内容
9．下面是四组线段的长度，哪一组能组成三角形（ ）| A． | 2，2，4 | B． | 5，5，5 | C． | 11，5，6 | D． | 3，8，24 |
分析 根据三角形的三边关系：三角形两边之和大于第三边进行分析即可．
解答 解：A、2+2=4，不能构成三角形，故此选项错误；
B、5+5＞5，能构成三角形，故此选项正确；
C、5+6=11，不能构成三角形，故此选项错误；
D、8+3＜24，不能构成三角形，故此选项错误；
故选：B．
点评 此题主要考查了三角形的三边关系，在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式，只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
20．下列说法中，正确的是（ ）
| A． | 0是最小的整数 | B． | 最大的负整数是-1 | ||
| C． | 任何有理数的绝对值都是正数 | D． | 一个有理数的平方总是正数 |
17．
如图，在平面直角坐标系中．矩形OABC的对角线OB，AC相交于点D，且BE∥AC，AE∥OB．如果OA=3，OC=2，则经过点E的反比例函数解析式为（ ）
如图，在平面直角坐标系中．矩形OABC的对角线OB，AC相交于点D，且BE∥AC，AE∥OB．如果OA=3，OC=2，则经过点E的反比例函数解析式为（ ）| A． | $y=\frac{9}{2x}$ | B． | $y=\frac{2}{9x}$ | C． | $y=\frac{{\sqrt{13}}}{x}$ | D． | $y=\frac{{\sqrt{13}}}{2x}$ |
14．某校八年级（1）班50名学生参加2007年济宁市数学质量监测考试，全班学生的成绩统计如下表：
请根据表中提供的信息解答下列问题：
（1）该班学生考试成绩的众数和中位数分别是多少？
（2）该班张华同学在这次考试中的成绩是83分，能不能说张华同学的成绩处于全班中偏上水平？试说明理由．
| 成绩（分） | 71 | 74 | 78 | 80 | 82 | 83 | 85 | 86 | 88 | 90 | 91 | 92 | 94 |
| 人数 | 1 | 2 | 3 | 5 | 4 | 5 | 3 | 7 | 8 | 4 | 3 | 3 | 2 |
（1）该班学生考试成绩的众数和中位数分别是多少？
（2）该班张华同学在这次考试中的成绩是83分，能不能说张华同学的成绩处于全班中偏上水平？试说明理由．
1．随意掷两个均匀的骰子，朝上面的点数之和是10的概率是（ ）
| A． | $\frac{1}{12}$ | B． | 1 | C． | $\frac{1}{18}$ | D． | 0 |
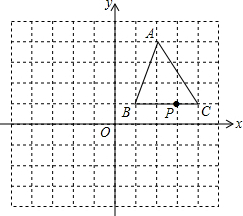如图，三角形ABC的顶点坐标分别为A（2，4）、B（1，1）、C（4，1）．BC上的一点P的坐标为P（3，1），将三角形ABC向左平移4个单位，再向上平移1个单位，得到三角形A1B1C1，其中点A、B、C、P分别对应点A1、B1、C1、P1．
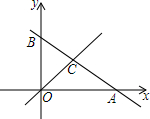如图，直线y1=-$\frac{1}{2}$x+2与x轴、y轴分别交于点A和点B，直线y2过原点O且与直线