题目内容
10.已知83=a9=2b,求(a-$\frac{1}{5}$b)2+(a+$\frac{1}{5}$b)2-2b(a2+$\frac{1}{25}$b)的值.分析 首先根据同底数幂的知识求出a和b的值,然后根据完全平方公式以及单项式乘以多项式运算法则去掉括号并合并同类项,最后代值计算.
解答 解:∵83=a9=2b,
∴(23)3=a9=2b,
∴a=2,b=9,
原式=(a-$\frac{1}{5}$b)2+(a+$\frac{1}{5}$b)2+2(a-$\frac{1}{5}$b)(a+$\frac{1}{5}$b)-2(a-$\frac{1}{5}$b)(a+$\frac{1}{5}$b)-2a2b-$\frac{2}{25}$b2
=(a-$\frac{1}{5}$b+a+$\frac{1}{5}$b)2-2(a2-$\frac{1}{25}$b2)-2a2b-$\frac{2}{25}$b2
=(2a)2-2a2+$\frac{2}{25}$b2-2a2b-$\frac{2}{25}$b2
=4a2-2a2-2a2b
=2a2-2a2b
=2a2(1-b),
所以把a=2,b=9代入化简的式子中得到原式=2×4(1-9)=-64.
点评 本题主要考查了整式的混合运算-化简求值的知识,解答本题的关键是熟练掌握完全平方公式以及多项式乘法的运算法则以及能根据非负数的性质求出a和b的值,此题难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20. 在菱形ABCD中,下列结论错误的是( )
在菱形ABCD中,下列结论错误的是( )
 在菱形ABCD中,下列结论错误的是( )
在菱形ABCD中,下列结论错误的是( )| A. | BO=DO | B. | ∠DAC=∠BAC | C. | AC⊥BD | D. | AO=DO |

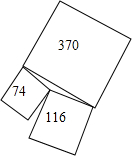 如图,三个正方形形状的土地面积分别为74英亩,116英亩,370英亩,三个正方形恰好围着一个池塘.现要将这550英亩的土地拍卖,如果有人能计算出池塘的面积,那么池塘不计入土地价钱白白奉送,英国数学家巴尔教授曾经巧妙地解答了这个问题,你能解答吗?
如图,三个正方形形状的土地面积分别为74英亩,116英亩,370英亩,三个正方形恰好围着一个池塘.现要将这550英亩的土地拍卖,如果有人能计算出池塘的面积,那么池塘不计入土地价钱白白奉送,英国数学家巴尔教授曾经巧妙地解答了这个问题,你能解答吗?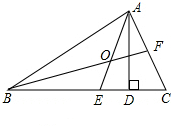 已知:如图,△ABC中,AD、AE分别是△ABC的高和角平分线,BF是∠ABC的平分线,BF与AE交于O,若∠ABC=40°,∠C=60°,求∠DAE、∠BOE的度数.
已知:如图,△ABC中,AD、AE分别是△ABC的高和角平分线,BF是∠ABC的平分线,BF与AE交于O,若∠ABC=40°,∠C=60°,求∠DAE、∠BOE的度数.