题目内容
3．把1000个黑球与白球按如图规律摆放，则黑球有44个，白球有956个．
分析 以黑球为分界，白球的规律是1，2，3，4，5．…，即第一个黑球后面是1个白球，第二个后面是2个白球，…依此类推第n个黑球的后面有n个白球，由此规律计算得出答案即可．
解答 解：∵第一个黑球后面是1个白球，
第二个后面是2个白球，
…
∴第n个黑球的后面有n个白球，
∴共有n+1+2+3+4+…n=n+$\frac{1}{2}$n（n+1）=$\frac{1}{2}$n（n+3），
∵$\frac{1}{2}$×43×46=989，$\frac{1}{2}$×44×47=1034，
∴1000个黑球与白球中黑球有43+1=44个，白球1000-44=956个．
故答案为：44，956．
点评 此题考查图形的变化规律，找出白球与黑球的排列规律，得出运算的方法是解决问题的关键．
练习册系列答案
特高级教师点拨系列答案
相关题目
18．小明业余时间进行飞镖训练，上周日训练的平均成绩是8.5环，而这一周训练的平均成绩变化如表：（单位：环）
注：正号表示比前一天提高，负号表示比前一天下降．
本周哪一天的平均成绩最高，它是多少环？
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 成绩 | +1 | +0.2 | -0.5 | +0.3 | +0.2 | -0.7 | -0.1 |
本周哪一天的平均成绩最高，它是多少环？
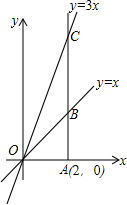如图所示，已知正比例函数y=x和y=3x，过点A（2，0）作x轴的垂线，与这两个正比例函数的图象分别交与B，C两点，求三角形OBC的面积（其中O为坐标原点）．