题目内容
20.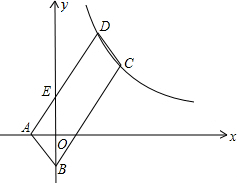 如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-2),顶点C、D在双曲线y=$\frac{k}{x}$上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的3倍.
如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-2),顶点C、D在双曲线y=$\frac{k}{x}$上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的3倍.(1)求证:AE=DE;
(2)求k的值.
分析 (1)利用已知四边形BCDE的面积是△ABE面积的3倍,得出平行四边形ABCD的面积是△ABE面积的4倍,则S△ABD=2S△ABE,再利用三角形中线的性质,平分面积进而得出答案;
(2)设E点坐标为(0,t),利用线段中点坐标公式得D点坐标为(1,2t),然后利用平移的性质得到点C(2,-2+2t),再利用反比例函数图象上点的坐标特征得k=1×2t=2×(-2+2t),解得t=2,进而求出k的值.
解答 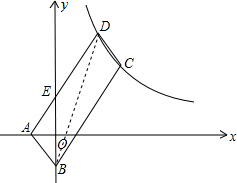 (1)证明:连结BD,如图,
(1)证明:连结BD,如图,
∵四边形EBCD的面积是△ABE面积的3倍,
∴平行四边形ABCD的面积是△ABE面积的4倍,
∴S△ABD=2S△ABE,
∴AD=2AE,即点E为AD的中点,
故AE=DE;
(2)解:设E点坐标为(0,t),
∵A点坐标为(-1,0),
∴D点坐标为(1,2t),
∵AB∥CD,且AB=CD,
而点A(-1,0)先向右平移2个单位,再向上平移2t个单位得到点D(1,2t),
∴点B(0,-2)先向右平移2个单位,再向上平移2t个单位得到点C(2,-2+2t),
把D(1,2t)、C(2,-2+2t)代入y=$\frac{k}{x}$得:
k=1×2t=2×(-2+2t),
解得:t=2,
则k=1×2×2=4.
点评 本题考查了反比例函数综合题:掌握反比例函数图象上点的坐标特征、平移的性质和平行四边形的性质等知识,根据题意表示出C,D点坐标是解题关键.

练习册系列答案
相关题目
9.多项式2x3-x2y2+y3+25的次数和项数分别是( )
| A. | 5次4项 | B. | 3次4项 | C. | 4次4项 | D. | 无法确定 |
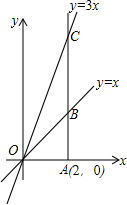 如图所示,已知正比例函数y=x和y=3x,过点A(2,0)作x轴的垂线,与这两个正比例函数的图象分别交与B,C两点,求三角形OBC的面积(其中O为坐标原点).
如图所示,已知正比例函数y=x和y=3x,过点A(2,0)作x轴的垂线,与这两个正比例函数的图象分别交与B,C两点,求三角形OBC的面积(其中O为坐标原点).