题目内容
已知两点A(-3,4)和B(3,-4),
(1)若抛物线y=ax2+bx+c经过A,B两点,求证:方程ax2+bx+c=0一定有两个不相等的实数根;
(2)试判断是否存在对称轴是y轴且经过A,B两点的抛物线,并证明你的结论.
(1)若抛物线y=ax2+bx+c经过A,B两点,求证:方程ax2+bx+c=0一定有两个不相等的实数根;
(2)试判断是否存在对称轴是y轴且经过A,B两点的抛物线,并证明你的结论.
考点:抛物线与x轴的交点
专题:
分析:(1)把点A、B的坐标代入函数解析式,求得a、b、c间的数量关系,然后再计算方程ax2+bx+c=0的根的判别式得到△=b2-4ac,根据非负数的性质得到△>0,然后根据判别式的意义即可得到方程ax2+bx+c=0一定有两个不相等的实数根.
(2)设该抛物线方程为y=kx2+t,然后把点A、B的坐标代入该抛物线方程,看方程组是否有解.
(2)设该抛物线方程为y=kx2+t,然后把点A、B的坐标代入该抛物线方程,看方程组是否有解.
解答:(2)证明:把点A(-3,4)和B(3,-4)分别代入y=ax2+bx+c,得
,
则
,
在方程ax2+bx+c=0中,
∵△=b2-4ac=
-4×(-
)c=
+
>0,
∴方程ax2+bx+c=0一定有两个不相等的实数根;
(2)解:不存在对称轴是y轴且经过A,B两点的抛物线,理由如下:
设该抛物线方程为y=kx2+t(k≠0),
把点A(-3,4)和B(3,-4),
代入该抛物线方程,得
,
该方程组无解,
故不存在这样的抛物线.
|
则
|
在方程ax2+bx+c=0中,
∵△=b2-4ac=
| 16 |
| 9 |
| c |
| 9 |
| 4c2 |
| 9 |
| 16 |
| 9 |
∴方程ax2+bx+c=0一定有两个不相等的实数根;
(2)解:不存在对称轴是y轴且经过A,B两点的抛物线,理由如下:
设该抛物线方程为y=kx2+t(k≠0),
把点A(-3,4)和B(3,-4),
代入该抛物线方程,得
|
该方程组无解,
故不存在这样的抛物线.
点评:本题考查了待定系数法求二次函数的解析式:常设二次函数的解析式有一般式、顶点式和交点式.也考查了一元二次方程根的判别式.

练习册系列答案
相关题目
在
、-
、-
、
中最大的数是( )
| 1 | |||
|
| 3 | 0.001 |
| 0.01 |
| 1 | ||
-
|
A、
| |||||
B、-
| |||||
C、-
| |||||
D、
|
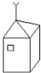 如图所示,从正面看,所能看到的结果是图形( )
如图所示,从正面看,所能看到的结果是图形( )A、 |
B、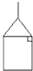 |
C、 |
D、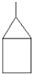 |
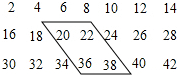 如图是由一些偶数排成的一个数阵.
如图是由一些偶数排成的一个数阵.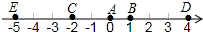 如图,A点的初始位置位于数轴上的原点.现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样,
如图,A点的初始位置位于数轴上的原点.现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样, 已知:如图,AD=BC,∠D=∠C.
已知:如图,AD=BC,∠D=∠C. 证明:等腰三角形底边中点到两腰距离相等.(请画出图形并写出已知、求证及证明过程)
证明:等腰三角形底边中点到两腰距离相等.(请画出图形并写出已知、求证及证明过程)