题目内容
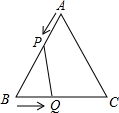 已知:如图所示,△ABC是边长6cm等边三角形,动点P、Q同时从A、B两点出发,分别在AB、BC边上均速移动,它们的速度分别为Vp=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t s
已知:如图所示,△ABC是边长6cm等边三角形,动点P、Q同时从A、B两点出发,分别在AB、BC边上均速移动,它们的速度分别为Vp=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t s(1)当t何值时,△PBQ为等边三角形?
(2)t何值时,△PBQ为直角三角形?
考点:等边三角形的判定与性质,勾股定理的逆定理
专题:动点型
分析:(1)由题意可知AP=2t,BQ=t,当△PBQ为等边三角形时,则有BP=BQ,即6-2t=t,可求得t;
(2)当PQ⊥BQ时,在Rt△PBQ中,BP=2PQ,可得6-2t=2t;当PQ⊥BP时,可得BQ=2BP,可得2t=2(6-2t)分别求得t的值即可.
(2)当PQ⊥BQ时,在Rt△PBQ中,BP=2PQ,可得6-2t=2t;当PQ⊥BP时,可得BQ=2BP,可得2t=2(6-2t)分别求得t的值即可.
解答:解:由题意可知AP=2t,BQ=t,则BP=AB-AP=6-2t,
(1)当△PBQ为等边三角形时,则有BP=BQ,即6-2t=t,解得t=2,即当t=2s时△PBQ为等边三角形;
(2)当PQ⊥BQ时,
∵∠B=60°,
∴∠BPQ=30°,
∴在Rt△PBQ中,BP=2PQ,
即6-2t=2t,
解得t=1.5;
当PQ⊥BP时,同理可得BQ=2BP,即t=2(6-2t),解得t=2.4,
综上可知当t为1.5s或2.4s时△PBQ为直角三角形.
(1)当△PBQ为等边三角形时,则有BP=BQ,即6-2t=t,解得t=2,即当t=2s时△PBQ为等边三角形;
(2)当PQ⊥BQ时,
∵∠B=60°,
∴∠BPQ=30°,
∴在Rt△PBQ中,BP=2PQ,
即6-2t=2t,
解得t=1.5;
当PQ⊥BP时,同理可得BQ=2BP,即t=2(6-2t),解得t=2.4,
综上可知当t为1.5s或2.4s时△PBQ为直角三角形.
点评:本题主要考查等边三角形的性质及判定和直角三角形的性质,利用t表示出BP和BQ,化“动”为“静”,是解题的关键.

练习册系列答案
相关题目
已知⊙O的半径为3cm,点P在⊙O内,则OP不可能等于( )
| A、1cm | ||
B、
| ||
| C、2cm | ||
| D、3cm |
下列说法错误的是( )
| A、零是绝对值最小的有理数 |
| B、如果两个数互为相反数,那么它们的绝对值相等 |
| C、任何有理数的绝对值都是非负数 |
| D、两个互为相反数的商是-1 |
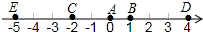 如图,A点的初始位置位于数轴上的原点.现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样,
如图,A点的初始位置位于数轴上的原点.现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样, 证明:等腰三角形底边中点到两腰距离相等.(请画出图形并写出已知、求证及证明过程)
证明:等腰三角形底边中点到两腰距离相等.(请画出图形并写出已知、求证及证明过程)