题目内容
18.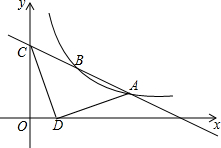 如图,已知一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象相交于A(4,1)、B(a,2)两点,一次函数的图象与y轴的交点为C.
如图,已知一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象相交于A(4,1)、B(a,2)两点,一次函数的图象与y轴的交点为C.(1)求反比例函数和一次函数的解析式;
(2)若点D的坐标为(1,0),求△ACD的面积.
分析 (1)首先把A(4,1)代入反比例函数解析式中确定k2,然后把B(a,2)代入反比例函数的解析式确定a,然后根据A,B两点坐标利用待定系数法确定一次函数的解析式;
(2)根据一次函数解析式求出其图象与坐标轴的交点坐标,然后用面积的割补法可以求出△ACD的面积.
解答 解:(1)把A(4,1)代入反比例函数y=$\frac{{k}_{2}}{x}$中,
∴k2=4×1=4,
∴y=$\frac{4}{x}$,
把B(a,2)代入求出的反比例函数解析式中得,n=2,
∴B(2,2),
把A(4,1),B(2,2)代入y=k1x+b得$\left\{\begin{array}{l}{4{k}_{1}+b=1}\\{2{k}_{1}+b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{1}=-\frac{1}{2}}\\{b=3}\end{array}\right.$.
∴一次函数解析式为y=-$\frac{1}{2}$x+3.
(2)设直线AB与x轴的交点为E,
当x=0时,y=3.当y=0时,x=6,
所以直线AB与坐标轴的交点坐标为C(0,3),E(6,0),
则S△ACD=S△EOC-S△DOC-S△ADE=$\frac{1}{2}$×6×3-$\frac{1}{2}$×1×3-$\frac{1}{2}$(6-1)×1=5.
点评 此题考查了用待定系数法确定反比例函数和一次函数的解析式,也考查了利用函数的性质求不规则图形的面积.

练习册系列答案
相关题目
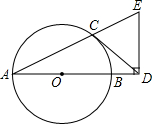 如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.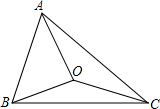 如图,CA=CB,OA=OB,求证:OC⊥AB.
如图,CA=CB,OA=OB,求证:OC⊥AB.