题目内容
15.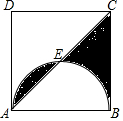 小明向如图所示的正方形ABCD区域内投掷飞镖,点E是以AB为直径的半圆与对角线AC的交点.如果小明投掷飞镖一次,则飞镖落在阴影部分的概率为( )
小明向如图所示的正方形ABCD区域内投掷飞镖,点E是以AB为直径的半圆与对角线AC的交点.如果小明投掷飞镖一次,则飞镖落在阴影部分的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{8}$ |
分析 直接利用正方形的性质结合转化思想得出阴影部分面积=S△CEB,进而得出答案.
解答  解:如图所示:连接BE,
解:如图所示:连接BE,
可得,AE=BE,∠AEB=90°,
且阴影部分面积=S△CEB=$\frac{1}{2}$S△BEC=$\frac{1}{4}$S正方形ABCD,
故小明投掷飞镖一次,则飞镖落在阴影部分的概率为:$\frac{1}{4}$.
故选:B.
点评 此题主要考查了几何概率,正确利用正方形性质得出阴影部分面积=S△CEB是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.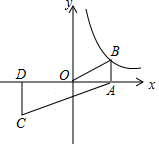 已知反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
已知反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(1)求这个反比函数的解析式;
(2)求△ACD的面积.
 已知反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
已知反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.(1)求这个反比函数的解析式;
(2)求△ACD的面积.
7. 如图,矩形ACBD中,AB=5,BC=12,AB的中垂线与BC交于点E,与AD交于F,则BE的长等于( )
如图,矩形ACBD中,AB=5,BC=12,AB的中垂线与BC交于点E,与AD交于F,则BE的长等于( )
 如图,矩形ACBD中,AB=5,BC=12,AB的中垂线与BC交于点E,与AD交于F,则BE的长等于( )
如图,矩形ACBD中,AB=5,BC=12,AB的中垂线与BC交于点E,与AD交于F,则BE的长等于( )| A. | $\frac{12}{5}$ | B. | $\frac{13}{5}$ | C. | $\frac{169}{24}$ | D. | $\frac{60}{13}$ |
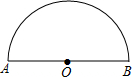 如图,AB是半圆O的直径,且AB=4cm,动点P从点O出发,沿OA→$\widehat{AB}$→BO的路径以每秒1cm的速度运动一周.设运动时间为t,s=OP2,则下列图象能大致刻画s与t的关系的是( )
如图,AB是半圆O的直径,且AB=4cm,动点P从点O出发,沿OA→$\widehat{AB}$→BO的路径以每秒1cm的速度运动一周.设运动时间为t,s=OP2,则下列图象能大致刻画s与t的关系的是( )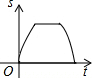




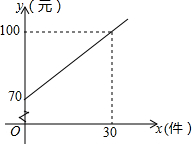 某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示.
某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示. 如图,正方形ABCD中内接正三角形AEF.求证:S△EFC=S△ABE+S△ADF.
如图,正方形ABCD中内接正三角形AEF.求证:S△EFC=S△ABE+S△ADF.