题目内容
19.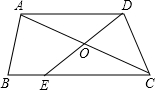 如图,在四边形ABCD中,AD∥BC,点O是对角线AC的中点,DO的延长线与BC相交于点E,设$\stackrel{→}{AB}$=$\stackrel{→}{a}$,$\stackrel{→}{AD}$=$\stackrel{→}{b}$,$\stackrel{→}{BE}$=$\stackrel{→}{c}$.
如图,在四边形ABCD中,AD∥BC,点O是对角线AC的中点,DO的延长线与BC相交于点E,设$\stackrel{→}{AB}$=$\stackrel{→}{a}$,$\stackrel{→}{AD}$=$\stackrel{→}{b}$,$\stackrel{→}{BE}$=$\stackrel{→}{c}$.(1)试用向量$\stackrel{→}{a}$、$\stackrel{→}{b}$、$\stackrel{→}{c}$表示下列向量:$\stackrel{→}{ED}$=-$\overrightarrow{a}$-$\overrightarrow{c}$+$\overrightarrow{b}$;
(2)写出图中所有与$\stackrel{→}{AD}$互为相反向量的向量:$\overrightarrow{DA}$和$\overrightarrow{CE}$;
(3)求作:$\stackrel{→}{AD}$+$\stackrel{→}{OC}$.(保留作图痕迹,写出结果,不要求写作法)
分析 (1)由$\overrightarrow{AB}$+$\overrightarrow{BE}$=$\overrightarrow{AD}$+$\overrightarrow{DE}$,推出$\overrightarrow{DE}$=$\overrightarrow{a}$+$\overrightarrow{c}$-$\overrightarrow{b}$,推出$\overrightarrow{ED}$=-$\overrightarrow{a}$-$\overrightarrow{c}$+$\overrightarrow{b}$;
(2)图中与$\stackrel{→}{AD}$互为相反向量的向量有$\overrightarrow{DA}$和$\overrightarrow{CE}$;
(3)如图,作DM∥OC,CM∥OD,则向量$\overrightarrow{AM}$即为所求;
解答 解:(1)∵$\overrightarrow{AB}$+$\overrightarrow{BE}$=$\overrightarrow{AD}$+$\overrightarrow{DE}$,
∴$\overrightarrow{DE}$=$\overrightarrow{a}$+$\overrightarrow{c}$-$\overrightarrow{b}$,
∴$\overrightarrow{ED}$=-$\overrightarrow{a}$-$\overrightarrow{c}$+$\overrightarrow{b}$.
故答案为-$\overrightarrow{a}$-$\overrightarrow{c}$+$\overrightarrow{b}$.
(2)图中与$\stackrel{→}{AD}$互为相反向量的向量有$\overrightarrow{DA}$和$\overrightarrow{CE}$,
故答案为$\overrightarrow{DA}$和$\overrightarrow{CE}$,
(3)如图,作DM∥OC,CM∥OD,
则向量$\overrightarrow{AM}$即为所求.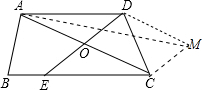
点评 本题考查平面向量的性质、三角形法则、平行四边形的性质等知识,解题的关键是熟练掌握基本概念,属于中考基础题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案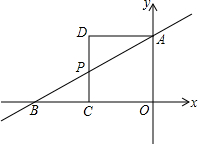 如图,在直角坐标系中,直线AB分别与x轴、y轴交于B、A两点,OA、OB的长是关于x的一元二次方程x2-12x+32=0的两个实数根,且OB>OA,以OA为一边作如图所示的正方形AOCD,CD交AB于点P.
如图,在直角坐标系中,直线AB分别与x轴、y轴交于B、A两点,OA、OB的长是关于x的一元二次方程x2-12x+32=0的两个实数根,且OB>OA,以OA为一边作如图所示的正方形AOCD,CD交AB于点P.
 如图,?ABCD的对角线AC、BD相交于点O,点E是CD的中点.
如图,?ABCD的对角线AC、BD相交于点O,点E是CD的中点.