题目内容
2. 如图,直角△ABC中,∠BAC=90°,AB=AC,BD=CD,BE平分∠ABC,FD⊥ED交AB于F,BE交AD于H,则下列结论:①AH=AE;②S四边形AFDE=$\frac{1}{2}$S△ABC;③BF2+CE2=EF2,其中正确的是( )
如图,直角△ABC中,∠BAC=90°,AB=AC,BD=CD,BE平分∠ABC,FD⊥ED交AB于F,BE交AD于H,则下列结论:①AH=AE;②S四边形AFDE=$\frac{1}{2}$S△ABC;③BF2+CE2=EF2,其中正确的是( )| A. | ①②③ | B. | ②③ | C. | ①② | D. | ①③ |
分析 根据三角形的外角性质可以证明∠AHE=∠AEH,故①正确;由△BDF≌△ADE得到S△BDF=S△ADE,所以S四边形AFDE=S△ABD=${\frac{1}{2}}_{\;}$S△ABC故②正确;只要证明BF=AE、CE=AF,即可证明③正确.
解答 解∵AB=AC,∠BAC=90°,BD=DC,
∴AD⊥BC,∠BAD=∠DAC=∠ABD=∠C=45°,
∴AD=BD=DC,
∵∠AHE=∠ABE+∠BAD,∠AEB=∠C+∠EBC
∵∠ABE=∠EBC,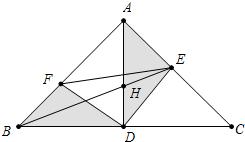
∴∠AHE=∠AEH,
∴AH=AE,故①正确;
∵∠BDF+∠ADF=90°,∠ADF+∠ADE=90°,
∴∠BDF=∠ADE,
在△BDF或△DAE中,
$\left\{\begin{array}{l}{∠FBD=∠DAE}\\{BD=DA}\\{∠BDF=∠ADE}\end{array}\right.$,
∴△BDF≌△ADE,
∴S△BDF=S△ADE,BF=AE,
∴S四边形AFDE=S△ABD=${\frac{1}{2}}_{\;}$S△ABC,故②正确;
同理可证:△ADF≌△CDE,
∴EC=AF,
在RT△AEF中,∵AF2+AE2=EF2,
∴EC2+CF2=EF2故③正确.
故选A.
点评 本题考查三角形外角的性质.全等三角形的判定和性质、四边形的面积问题等知识,寻找全等三角形是解决问题的关键.

练习册系列答案
相关题目
2. 如图,在边长为1个单位长度的小正方形网格中,点A、B都是格点(即网格线的交点),则线段AB的长度为( )
如图,在边长为1个单位长度的小正方形网格中,点A、B都是格点(即网格线的交点),则线段AB的长度为( )
 如图,在边长为1个单位长度的小正方形网格中,点A、B都是格点(即网格线的交点),则线段AB的长度为( )
如图,在边长为1个单位长度的小正方形网格中,点A、B都是格点(即网格线的交点),则线段AB的长度为( )| A. | 3$\sqrt{3}$ | B. | 5 | C. | 6 | D. | 4$\sqrt{2}$ |
7.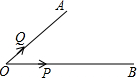 如图,在∠AOB=30°的两边上有两点P和Q在运动,且点P从离点O有1厘米远的地方出发,以1厘米每秒运动,点Q从点O出发以2厘米每秒运动,则△POQ为等腰三角形时,两点的运动时间为( )秒.
如图,在∠AOB=30°的两边上有两点P和Q在运动,且点P从离点O有1厘米远的地方出发,以1厘米每秒运动,点Q从点O出发以2厘米每秒运动,则△POQ为等腰三角形时,两点的运动时间为( )秒.
 如图,在∠AOB=30°的两边上有两点P和Q在运动,且点P从离点O有1厘米远的地方出发,以1厘米每秒运动,点Q从点O出发以2厘米每秒运动,则△POQ为等腰三角形时,两点的运动时间为( )秒.
如图,在∠AOB=30°的两边上有两点P和Q在运动,且点P从离点O有1厘米远的地方出发,以1厘米每秒运动,点Q从点O出发以2厘米每秒运动,则△POQ为等腰三角形时,两点的运动时间为( )秒.| A. | $1;2\sqrt{3}+3;\frac{{2\sqrt{3}+1}}{11}$ | B. | $1;2\sqrt{3}+3;\frac{{2\sqrt{3}+1}}{13}$ | C. | $1;2\sqrt{3}+3$;5 | D. | 以上都不对 |
 如图,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在AB上.
如图,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在AB上. 如图,点O是等边△ABC内一点.∠COB=140°,∠AOB=α,将△COB绕点C按顺时针方向旋转60°得△ADC,连接OD
如图,点O是等边△ABC内一点.∠COB=140°,∠AOB=α,将△COB绕点C按顺时针方向旋转60°得△ADC,连接OD