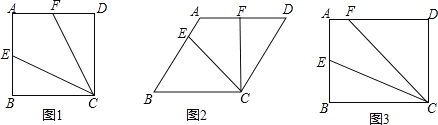
题目内容
【题目】如图,在矩形ABCD中,AB=4,BC=10,P为射线AB上一点,连接PD、AC,且PD、AC交于点E,过点A作AF⊥PD,垂足为点F.
(1)当点F落在BC边上时,求AP的值
(2)当△PAE为等腰三角形时,求AP的值.

【答案】(1)5或20(2)![]() 或
或![]() 或4
或4
【解析】
(1)先判断出△ABF∽△FCD,进而求出BF=2或8,再判断出△ABF∽△FBP,得出比例式建立方程即可得出结论;
(2)分三种情况,利用等腰三角形的性质和勾股定理,即可得出结论.
(1)如图1,
∵∠AFD=90°,
∴∠AFB+∠CFD=90°,
∵四边形ABCD是矩形,
∴∠DCF=∠ABC=90°,
∴∠AFB+∠BAF=90°,
∴∠BAF=∠CFD,
∵∠ABF=∠FCD=90°,
∴△ABF∽△FCD,
![]()
![]()
∴BF=2或BF=8,
∵AF⊥PD,∴∠PFB+∠AFB=90°,
∵∠FPB+∠PFB=90°,
∴∠AFB=∠FPB
∵∠ABF=∠FBP=90°
∴△ABF∽△FBP,
![]()
![]() 或
或![]()
∴AP=5或AP=20;
(2)∵△PAE为等腰三角形,
∴①当PA=PE时,
∴∠PAE=∠PEA,
∵AB∥CD,
∴∠PAE=∠DCE,
∴∠DEC=∠DCE,
∴DE=CD=4,
∴DP=PE+DE=PA+4
在Rt△ADP中,根据勾股定理得,PD2=AD2+AP2,
∴(AP+4)2=100+PA2,
![]()
②当PA=AE时,
∴∠APE=∠AEP,
∵AB∥CD,
∴∠APE=∠CDE,
∵∠AEP=∠CED,
∴∠CDE=∠CED,
∴CE=CD=4,
∴AC=AP+4,
在Rt△ABC中,根据勾股定理得,(AP+4)2=16+100,
![]() (舍去)或
(舍去)或![]()
③当PE=AE时,∴∠APE=∠PAE,
∵AB∥CD,
∴∠APE=∠CDE,∠PAE=∠DCE,
∴CE=DE,
∴PE+DE=AE+CE=AC,
∴点P和点B重合,
即:AP=AB=4,
∴AP=4,
综上所述,当△PAE为等腰三角形时,AP的值为![]() 或
或![]() 或4
或4

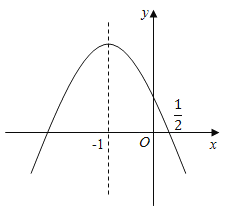
【题目】已知函数![]() ,
,![]() ,探究函数图象和性质过程如下:
,探究函数图象和性质过程如下:
(1)下表是y与x的几组值,则解析式中的m= ,表格中的n= ;
x | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y |
|
|
| 1 |
| 3 |
| 4 |
| 3 | n | 0 | … |
(2)在平面直角坐标系中描出表格中各点,并画出函数图象:
(3)若A(x1,y1)、B(x2,y2)、C(x3,y3)为函数图象上的三个点,其中x2+x3>4且﹣1<x1<0<x2<2<x3<4,则y1、y2、y3之间的大小关系是 ;
(4)若直线y=k+1与该函数图象有且仅有一个交点,则k的取值范围为 .