Question

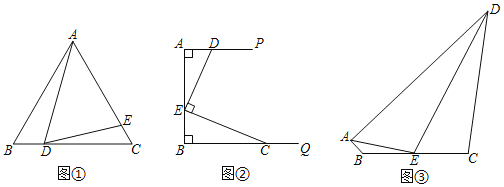
【题目】在四边形ABCD中，点E、F分别是AB、AD边上一点，∠DFC＝2∠FCE．

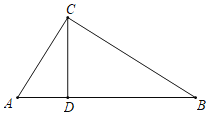
（1）如图1，若四边形ABCD是正方形，∠DFC＝60°，BE＝4，则AF＝　 　．

（2）如图2，若四边形ABCD是菱形，∠A＝120°，∠DFC＝90°，BE＝4，求的值．

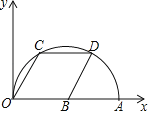
（3）如图3，若四边形ABCD是矩形，点E是AB的中点，CE＝12，CF＝13，求的值．

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）根据含30°的直角三角形的性质解答即可；

（2）过E作EG⊥BC，利用含30°的直角三角形的性质和等腰直角三角形的性质进行解答即可；

（3）延长FE交CB延长线于点M，再利用相似三角形的性质和勾股定理进行解答．

解：（1）∵四边形ABCD是正方形，∠DFC＝60°，

∴∠DCF＝30°，

∵∠DFC＝2∠FCE，

∴∠FCE＝∠ECB＝30°，

∴

∴DF＝4，

∴

故答案为：

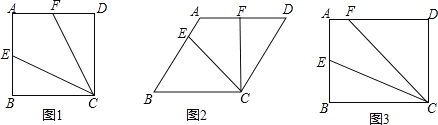
（2）过E作EG⊥BC，如图1：

∵∠DFC＝90°，∠DFC＝2∠FCE，

∴∠FCE＝∠BCE＝45°，

∵∠A＝120°，

∴∠B＝60°，

∴BG＝2，

∴

∴BC＝CD＝AB＝AD＝

∴

∴

∴

∴

（3）延长FE交CB延长线于点M，如图2：

在△AFE与△BME中，

∴△AFE≌△BME（ASA），

∴BM＝AF，ME＝EF，

∵∠DFC＝2∠FCE，

∴CE是∠FCB的角平分线，

∴CM＝CF＝13，

在Rt△MEC中，，

∵∠EMB＝∠EMB，∠EBM＝∠EBC＝90°，

∴△EMB∽△EMC，

∴．