题目内容
20. 如图所示,已知⊙O的半径为13,点O到AB的距离是5,则弦AB长为24.
如图所示,已知⊙O的半径为13,点O到AB的距离是5,则弦AB长为24.
分析 过点O作OD⊥AB于点D,则AB=2AD,再由勾股定理求出AD的长,进而可得出结论.
解答 解:过点O作OD⊥AB于点D,则AB=2AD,
∵⊙O的半径为13,点O到AB的距离是5,
∴AD=$\sqrt{O{A}^{2}-O{D}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
∴AB=2AD=24.
故答案为:24.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
10.已知一次函数y=kx+b,经过A(0,3),B(1,2)两点,则它的图象经过( )
| A. | 第一、二、三象限 | B. | 第一、三、四象限 | C. | 第一、二、四象限 | D. | 第二、三、四象限 |
11.方程2x-3=5解是( )
| A. | 4 | B. | 5 | C. | 3 | D. | 6 |
8.曲阜市某天的最高气温9℃,最低气温-2℃,这一天曲阜市的温差是( )
| A. | 11℃ | B. | -11℃ | C. | 7℃ | D. | -7℃ |
15.以下列各组长度的线段为边,能构成三角形的是( )
| A. | 3cm、4cm、8cm | B. | 5cm、5cm、10cm | C. | 12cm、5cm、6cm | D. | 8cm、6cm、4cm |
12. 如图,在△ABC中,AB=AC,∠ABC=72°,CD平分∠ACB,BO平分∠ABC交CD于O点,则∠DOB的度数是( )
如图,在△ABC中,AB=AC,∠ABC=72°,CD平分∠ACB,BO平分∠ABC交CD于O点,则∠DOB的度数是( )
 如图,在△ABC中,AB=AC,∠ABC=72°,CD平分∠ACB,BO平分∠ABC交CD于O点,则∠DOB的度数是( )
如图,在△ABC中,AB=AC,∠ABC=72°,CD平分∠ACB,BO平分∠ABC交CD于O点,则∠DOB的度数是( )| A. | 36° | B. | 54° | C. | 72° | D. | 108° |
9.用配方法解方程x2-2x-1=0时,原方程应变形为( )
| A. | (x-1)2=0 | B. | (x-1)2=1 | C. | (x-1)2=2 | D. | (x-1)2=5 |
10.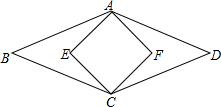 如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为( )
如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为( )
 如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为( )
如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为( )| A. | 10cm | B. | 13cm | C. | 15cm | D. | 24cm |