题目内容
12．
如图，在△ABC中，AB=AC，∠ABC=72°，CD平分∠ACB，BO平分∠ABC交CD于O点，则∠DOB的度数是（ ）| A． | 36° | B． | 54° | C． | 72° | D． | 108° |
分析 根据角平分线的定义和等腰三角形的性质求出∠OBC，∠OCB的值，再利用三角形外角的性质求出∠DOB的度数．
解答 解：∵在△ABC中，AB=AC，∠ABC=72°，
∴∠ACB=72°，
∵CD平分∠ACB，BO平分∠ABC，
∴∠OBC=36°，∠OCB=36°，
∴∠DOB=36°+36°=72°．
故选：C．
点评 本题考查了等腰三角形的性质，将三角形外角的性质和角平分线的性质相结合，是一道常见题，需要认真对待．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
3．观察如图汽车图标，其中既是轴对称图形又是中心对称图形的有（ ）个．
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
如图所示，已知⊙O的半径为13，点O到AB的距离是5，则弦AB长为24．
7．27的立方根是（ ）
| A． | -3 | B． | -9 | C． | 3 | D． | 9 |
17．若把分式$\frac{x+y}{2xy}$中的x和y都扩大10倍，那么分式的值（ ）
| A． | 扩大10倍 | B． | 不变 | C． | 缩小10倍 | D． | 缩小100倍 |
4．
如图，直线l1∥l2∥l3，直线AC分别交l1，l2，l3于点A，B，C；直线DF分别交l1，l2，l3于点D、E、F，AC与DF相交于点H，且AH=2，HB=1，BC=5，则$\frac{DE}{EF}$=（ ）
如图，直线l1∥l2∥l3，直线AC分别交l1，l2，l3于点A，B，C；直线DF分别交l1，l2，l3于点D、E、F，AC与DF相交于点H，且AH=2，HB=1，BC=5，则$\frac{DE}{EF}$=（ ）| A． | $\frac{3}{5}$ | B． | 2 | C． | $\frac{2}{5}$ | D． | $\frac{1}{2}$ |
1．
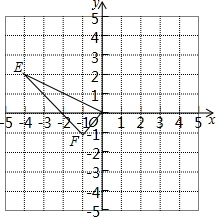如图所示，E（-4，2），F（-1，-1），以O为位似中心，按比例1：2把△EFO缩小，则点E的对应点E′的坐标为（ ）
如图所示，E（-4，2），F（-1，-1），以O为位似中心，按比例1：2把△EFO缩小，则点E的对应点E′的坐标为（ ）| A． | （2，-1）或（-2，1） | B． | （8，-4）或（-8，4） | C． | （2，-1） | D． | （8，-4） |
2．在下列图案中，是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |