题目内容
4.已知一次函数的图象经过点P(1,-3),且与x轴交于点A,与y轴交于点B,过P点作PE垂直于x轴于E,且PE:AE=3:5.(1)求这个一次函数的解析式;
(2)求一次函数的图象与两坐标轴所围成的图形的面积.
分析 (1)先利用PE⊥x轴得到E(1,0),PE=3,再利用PE:AE=3:5得到AE=5,所以A点坐标为(6,0)或(-4,0),然后分两种情况利用待定系数法求一次函数解析式;
(2)对于(1)中的两个解析式,分别求出对应的B点坐标,然后根据三角形面积公式计算.
解答 解:(1)∵P(1,-3),PE⊥x轴,
∴E(1,0),PE=3,
∵PE:AE=3:5,
∴AE=5,
∴A点坐标为(6,0)或(-4,0),
设一次函数解析式为y=kx+b,
当A点坐标为(6,0)时,把A(6,0),P(1,-3)代入得$\left\{\begin{array}{l}{6k+b=0}\\{k+b=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{3}{5}}\\{b=-\frac{18}{5}}\end{array}\right.$,此时一次函数解析式为y=$\frac{3}{5}$x-$\frac{18}{5}$;
当A点坐标为(-4,0)时,把A(6,0),P(1,-3)代入得$\left\{\begin{array}{l}{-4k+b=0}\\{k+b=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{3}{5}}\\{b=-\frac{12}{5}}\end{array}\right.$,此时一次函数解析式为y=-$\frac{3}{5}$x-$\frac{12}{5}$;
∴一次函数解析式为y=$\frac{3}{5}$x-$\frac{18}{5}$或y=-$\frac{3}{5}$x-$\frac{12}{5}$;
(2)当y=0时,y=$\frac{3}{5}$x-$\frac{18}{5}$=-$\frac{18}{5}$,则B(0,-$\frac{18}{5}$),则一次函数的图象与两坐标轴所围成的图形的面积=$\frac{1}{2}$×6×$\frac{18}{5}$=$\frac{54}{5}$;
当y=0时,y=-$\frac{3}{5}$x-$\frac{12}{5}$=-$\frac{12}{5}$,则B(0,-$\frac{12}{5}$),则一次函数的图象与两坐标轴所围成的图形的面积=$\frac{1}{2}$×4×$\frac{12}{5}$=$\frac{24}{5}$.
点评 本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;再将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;然后解方程或方程组,求出待定系数的值,进而写出函数解析式.

| A. | 0.831×108 | B. | 8.31×106 | C. | 8.31×107 | D. | 83.1×106 |
| A. | 8.18×109 | B. | 8.18×1010 | C. | 8.18×1011 | D. | 0.818×1011 |
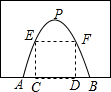 2015年以来.安徽省高速公路建设稳步推进,相继有十条高速公路建成通车.实现了所有的县在半小时内通达高速.全省高速公路通车里程突破4200公里.如图是某高速单向过山隧道截面设计图.隧道横截面呈抛物线形,设计AB=6米,最高点P点距地面8米.
2015年以来.安徽省高速公路建设稳步推进,相继有十条高速公路建成通车.实现了所有的县在半小时内通达高速.全省高速公路通车里程突破4200公里.如图是某高速单向过山隧道截面设计图.隧道横截面呈抛物线形,设计AB=6米,最高点P点距地面8米. 如图,直线y=x+a-5与双曲线y=$\frac{8}{x}$交于A,B两点,则当线段AB的长度取最小值时,a的值为5.
如图,直线y=x+a-5与双曲线y=$\frac{8}{x}$交于A,B两点,则当线段AB的长度取最小值时,a的值为5.