题目内容
17.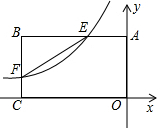 如图,反比例函数y=$\frac{k}{x}$(k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(-1,2).
如图,反比例函数y=$\frac{k}{x}$(k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(-1,2).(1)求反比例函数的解析式;
(2)连接EF,求△BEF的面积.
分析 (1)将E(-1,2)代入y=$\frac{k}{x}$,利用待定系数法即可求出反比例函数的解析式;
(2)由矩形的性质及已知条件可得B(-3,2),再将x=-3代入y=-$\frac{2}{x}$,求出y的值,得到CF=$\frac{2}{3}$,那么BF=2-$\frac{2}{3}$=$\frac{4}{3}$,然后根据△BEF的面积=$\frac{1}{2}$BE•BF,将数值代入计算即可.
解答 解:(1)∵反比例函数y=$\frac{k}{x}$(k<0)的图象过点E(-1,2),
∴k=-1×2=-2,
∴反比例函数的解析式为y=-$\frac{2}{x}$;
(2)∵E(-1,2),
∴AE=1,OA=2,
∴BE=2AE=2,
∴AB=AE+BE=1+2=3,
∴B(-3,2).
将x=-3代入y=-$\frac{2}{x}$,得y=$\frac{2}{3}$,
∴CF=$\frac{2}{3}$,
∴BF=2-$\frac{2}{3}$=$\frac{4}{3}$,
∴△BEF的面积=$\frac{1}{2}$BE•BF=$\frac{1}{2}$×2×$\frac{4}{3}$=$\frac{4}{3}$.
点评 本题考查了反比例函数与一次函数的交点问题,待定系数法求反比例函数的解析式,矩形的性质,三角形的面积,正确求出BF的值是解决第(2)小题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
7.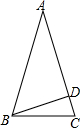 如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )
如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )
 如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )
如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )| A. | 36° | B. | 54° | C. | 18° | D. | 64° |
8.已知一组数据2,3,4,x,1,4,3有唯一的众数4,则这组数据的平均数、中位数分别是( )
| A. | 4,4 | B. | 3,4 | C. | 4,3 | D. | 3,3 |
5.用配方法解一元二次方程x2-6x-4=0,下列变形正确的是( )
| A. | (x-6)2=-4+36 | B. | (x-6)2=4+36 | C. | (x-3)2=-4+9 | D. | (x-3)2=4+9 |
2.一组数据6,-3,0,1,6的中位数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 6 |
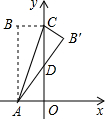 如图,矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则D点的坐标为(0,2.1).
如图,矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则D点的坐标为(0,2.1). 如图,在⊙O的内接四边形ABCD中,点E在DC的延长线上.若∠A=50°,则∠BCE=50°.
如图,在⊙O的内接四边形ABCD中,点E在DC的延长线上.若∠A=50°,则∠BCE=50°.