题目内容
(1)(-22)3
(2)(-x3)2(-x2)3
(3)(-
ab2)3
(4)(a2n-2)2•(an+1)3
(5)(-x5)4+(-x4)5
(6)(-2a)6-(-3a3)2+[-(2a)2]3
(7)(m-n)2(n-m)2(n-m)3
(8)x3•xn-1-xn-2•x4+xn+2
(9)-a2•(-a)2•(-a)2k•(-a)2k+1
(10)-(3x2y2)-(-3x)2•(-y)4•(x2y)2.
(2)(-x3)2(-x2)3
(3)(-
| 1 |
| 2 |
(4)(a2n-2)2•(an+1)3
(5)(-x5)4+(-x4)5
(6)(-2a)6-(-3a3)2+[-(2a)2]3
(7)(m-n)2(n-m)2(n-m)3
(8)x3•xn-1-xn-2•x4+xn+2
(9)-a2•(-a)2•(-a)2k•(-a)2k+1
(10)-(3x2y2)-(-3x)2•(-y)4•(x2y)2.
考点:幂的乘方与积的乘方,同底数幂的乘法
专题:
分析:根据同底数幂的乘法,幂的乘方,积的乘方的定义解答.
解答:解:(1)(-22)3=-26;
(2)(-x3)2(-x2)3
=-x6•x6
=-x12;
(3)(-
ab2)3=-
a3b6;
(4)(a2n-2)2•(an+1)3
=a4n-4•a3n+3
=a7n-1;
(5)(-x5)4+(-x4)5
=x20-x20
=0;
(6)(-2a)6-(-3a3)2+[-(2a)2]3
=(-2a)6-(-3a3)2+[-(2a)2]3
=64a6-9a6-64a6
=-9a6.
(7)(m-n)2(n-m)2(n-m)3
=(n-m)2(n-m)2(n-m)3
=(n-m)7;
(8)x3•xn-1-xn-2•x4+xn+2
=xn+2-xn+2+xn+2
=xn+2;
(9)-a2•(-a)2•(-a)2k•(-a)2k+1
=a4k+5;
(10)-(3x2y2)-(-3x)2•(-y)4•(x2y)2
=-(3x2y2)-9x2•y4•x4y2
=-3x2y2-9x6y6.
(2)(-x3)2(-x2)3
=-x6•x6
=-x12;
(3)(-
| 1 |
| 2 |
| 1 |
| 8 |
(4)(a2n-2)2•(an+1)3
=a4n-4•a3n+3
=a7n-1;
(5)(-x5)4+(-x4)5
=x20-x20
=0;
(6)(-2a)6-(-3a3)2+[-(2a)2]3
=(-2a)6-(-3a3)2+[-(2a)2]3
=64a6-9a6-64a6
=-9a6.
(7)(m-n)2(n-m)2(n-m)3
=(n-m)2(n-m)2(n-m)3
=(n-m)7;
(8)x3•xn-1-xn-2•x4+xn+2
=xn+2-xn+2+xn+2
=xn+2;
(9)-a2•(-a)2•(-a)2k•(-a)2k+1
=a4k+5;
(10)-(3x2y2)-(-3x)2•(-y)4•(x2y)2
=-(3x2y2)-9x2•y4•x4y2
=-3x2y2-9x6y6.
点评:本题考查了合并同类项,同底数幂的乘法,幂的乘方,积的乘方,理清指数的变化是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
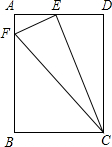 已知:如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连接FC.(AB>AE)
已知:如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连接FC.(AB>AE)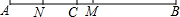 阅读并完成下列的计算过程:
阅读并完成下列的计算过程: