题目内容
如图,已知A、B、C、D四点均在以BC为直径的⊙O上,AD∥BC,AC平分∠BCD,∠ADC=120°,BC=4.

(1)求扇形ODC的面积;
(2)求四边形ABCD的周长.
(1) ;(2)10.
;(2)10.
【解析】
试题分析:(1)首先利用平行线的性质得出∠DCO=60°,进而得出△OCD是正三角形,再利用扇形面积公式求出即可;
(2)利用角平分线的性质得出∠3=∠1=∠2=30°,进而得出AD=DC=OC=2,即可得出四边形ABCD的周长.
试题解析:(1) ∵AD∥BC,∠ADC=120°,
∴∠DCO=60°,
又∵OC=OD,
∴△OCD是正三角形,
∴∠DOC=60°,
∴S扇形ODC=

(2)∵AD∥BC,AC平分∠BCD,
∴∠3=∠1=∠2=30°,
∴AD=DC=OC=2,
又∵BC为⊙O的直径,
∴∠BAC=90°,
又∵∠1=30°,
∴AB= BC=2,
BC=2,
∴四边形ABCD的周长为:AB+BC+CD+DA=10.
考点:1.扇形面积的计算;2.等边三角形的判定与性质;3.含30度角的直角三角形;4.圆周角定理.

练习册系列答案
相关题目


 B.
B. C.
C. D.
D.
 与反比例函数
与反比例函数 在同一平面直角坐标系中的图象如图所示,则当
在同一平面直角坐标系中的图象如图所示,则当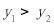 时
时 的取值范围是_________.
的取值范围是_________.
 时,抛物线
时,抛物线 的顶点在( )
的顶点在( ) 与
与 成反比例,当
成反比例,当 =2时,
=2时, =-1,求函数解析式和自变量
=-1,求函数解析式和自变量 的取值范围。
的取值范围。