题目内容
8.先化简($\frac{{a}^{2}}{a-2}$-$\frac{1}{a-2}$)÷$\frac{{a}^{2}-2a+1}{a-2}$,然后从1,2,3中选取一个你认为合适的数作为a的值代入求值.分析 先将分式进行化简,然后从a=1,2,3中挑出一个合适的数代入求解即可.
解答 解:原式=$\frac{{a}^{2}-1}{a-2}$×$\frac{a-2}{(a-1)^{2}}$
=$\frac{(a+1)(a-1)}{(a-1)^{2}}$
=$\frac{a+1}{a-1}$.
∵原式中分母有a-2、a-1,
∴a=3,
当a=3时,原式=$\frac{3+1}{3-1}$=2.
点评 本题考查了分式的化简求值,解答本题的关键在于将原式进行化简,并根据所得式子求出a≠1和2,然后将a=3代入求解.

练习册系列答案
相关题目
19.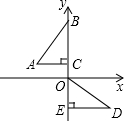 如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )
 如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )| A. | △ABC绕点C逆时针旋转90°,再向下平移1 | |
| B. | △ABC绕点C逆时针旋转90°,再向下平移3 | |
| C. | △ABC绕点C顺时针旋转90°,再向下平移1 | |
| D. | △ABC绕点C顺时针旋转90°,再向下平移3 |
16.二次函数y=x2的图象向右平移2个单位,得到新的函数图象的表达式是( )
| A. | y=x2-2 | B. | y=(x-2)2 | C. | y=x2+2 | D. | y=(x+2)2 |
3.若分式$\frac{{x}^{2}-9}{x-3}$的值为0,则x的值等于( )
| A. | 0 | B. | ±3 | C. | 3 | D. | -3 |
13.关于x的一元二次方程kx2-6x+1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k<9且k≠0 | B. | k<9 | C. | k≤9且k≠0 | D. | k≥9 |
 如图,在Rt△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,若DE垂直平分AB,交AB于点E,则∠B=30°.
如图,在Rt△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,若DE垂直平分AB,交AB于点E,则∠B=30°.