题目内容
17.已知有理数a,b,c满足|a2-1|+(b+3)2=-(3c-1)2n(n为正整数),则a-bc的值为多少?分析 根据非负数的性质可知a2-1=0,b+3=0,3c-1=0,求出a、b、c的值代入计算即可得到答案.
解答 解:∵|a2-1|+(b+3)2=-(3c-1)2n,
∴|a2-1|+(b+3)2+(3c-1)2n=0,
∴a2-1=0,b+3=0,3c-1=0,
解得a=±1,b=-3,c=$\frac{1}{3}$,
a-bc=0或2.
点评 本题考查的是非负数的性质,掌握几个非负数的和为0时,这几个非负数都为0是解题的关键,掌握一个数的绝对值和偶次方都是非负数.

练习册系列答案
相关题目
2.下列计算正确的是( )
| A. | $\sqrt{4}$+$\sqrt{5}$=$\sqrt{9}$ | B. | $\sqrt{(-2)^{2}}$=-2 | C. | $\sqrt{18}$÷3=$\sqrt{6}$ | D. | 3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$ |
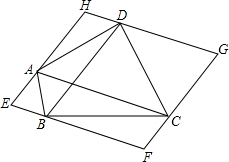 如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,得到四边形EFGH.
如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,得到四边形EFGH.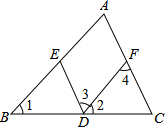 如图,已知∠1=∠2,∠A=∠3,AC与ED平行吗?填空并填写适当的理由.
如图,已知∠1=∠2,∠A=∠3,AC与ED平行吗?填空并填写适当的理由.