题目内容
如图，AD是△ABC的高，AE是△ABC的外接圆的直径，AB=10，AC=9，AD=6，求⊙O的半径．考点：圆周角定理,相似三角形的判定与性质
专题：计算题
分析：连结BE，如图，根据圆周角定理得到∠ABE=90°，∠E=∠C，于是可证明Rt△ABE∽Rt△ADC，然后利用相似比可计算出AE．
解答：解：连结BE，如图，
∵AE为直径，
∴∠ABE=90°，
∵AD⊥BC，
∴∠ADC=90°，
∵∠E=∠C，
∴Rt△ABE∽Rt△ADC，
∴
=
，即
=
，
∴AE=15，
∴⊙O的半径为
．
∵AE为直径，
∴∠ABE=90°，
∵AD⊥BC，
∴∠ADC=90°，
∵∠E=∠C，
∴Rt△ABE∽Rt△ADC，
∴
| AE |
| AC |
| AB |
| AD |
| AE |
| 9 |
| 10 |
| 6 |
∴AE=15，
∴⊙O的半径为
| 15 |
| 2 |
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．也考查了相似三角形的判定与性质．
练习册系列答案
相关题目
函数y=k1x+b与函数y=
如图，点G是△ADE边AE边上的中点（G是AE的二等分点），点D、E、F是△ABC边BC上四等分点，已知△ABC的面积为24cm2，则阴影部分的三角形的面积为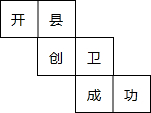
小林同学在正方体盒子的每个面上都写了一个字，分别是开、县、创、卫、成、功，其平面展开图如图所示，那么该正方体盒子上，“开”相对的面上所写的文字是
如图所示，要使图中平面展开图按虚线折叠成正方体后，相对面上两个数之和相等，则a+b+c=