题目内容
图1是棱长为a的小正方体,图2、图3由这样的小正方体摆放而成.按照这样的方法继续摆放,由上而下分别叫第一层、第二层、…、第n层,第n层的小正方体的个数为s.解答下列问题:
(1)按照要求填表:
(2)写出当n=10时,s= ;
(3)摆放成图3时,表面积是多少?

(1)按照要求填表:
| n | 1 | 2 | 3 | 4 | … | n |
| s | 1 | 3 | 6 | … |
(3)摆放成图3时,表面积是多少?
考点:规律型:图形的变化类
专题:
分析:(1)第1个图有1层,共1个小正方体,第2个图有2层,第2层正方体的个数为1+2…根据相应规律可得第n层正方体的个数为1+2+3+…+n=
;
(2)依据(1)得到的规律可得第10层正方体的个数;
(3)根据上、下、左、右、前、后看到小正方形的面的个数各为6,求出总面数再乘每一个小正方形的面积即可.
| n(n+1) |
| 2 |
(2)依据(1)得到的规律可得第10层正方体的个数;
(3)根据上、下、左、右、前、后看到小正方形的面的个数各为6,求出总面数再乘每一个小正方形的面积即可.
解答:解:(1)第1个图有1层,共1个小正方体,
第2个图有2层,第2层正方体的个数为1+2=3,
第4个图有4层,第4层正方体的个数为:1+2+3+4=10,
…
第n层正方体的个数为s=1+2+3+…+n=
;
(2)当n=10时,s=
=55;
(3)表面积是(6+6+6)×2×a2=36a2.
第2个图有2层,第2层正方体的个数为1+2=3,
第4个图有4层,第4层正方体的个数为:1+2+3+4=10,
…
第n层正方体的个数为s=1+2+3+…+n=
| n(n+1) |
| 2 |
| n | 1 | 2 | 3 | 4 | … | n | ||
| s | 1 | 3 | 6 | 10 | … |
|
| 10×(10+1) |
| 2 |
(3)表面积是(6+6+6)×2×a2=36a2.
点评:此题考查图形规律性的变化;得到第n层正方体的个数的规律是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知二次函数y=ax2+bx+c(a≠0)图象如图所示,且与x轴交于A(-1,0)、B(x1,0)两点,2<x1<3,给出下列结论:则正确的有
已知二次函数y=ax2+bx+c(a≠0)图象如图所示,且与x轴交于A(-1,0)、B(x1,0)两点,2<x1<3,给出下列结论:则正确的有 如图,阴影部分的面积用含有a,b的代数式表示为
如图,阴影部分的面积用含有a,b的代数式表示为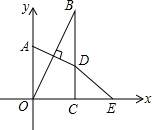 已知,如图在直角坐标系中,点A在y轴上,BC⊥x轴于点C,点A关于直线OB的对称点D恰好在BC上,点E与点O关于直线BC对称,∠OBC=35°,则∠OED=
已知,如图在直角坐标系中,点A在y轴上,BC⊥x轴于点C,点A关于直线OB的对称点D恰好在BC上,点E与点O关于直线BC对称,∠OBC=35°,则∠OED=