题目内容
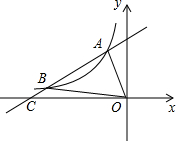 如图,一次函数y=kx+
如图,一次函数y=kx+| 5 |
| 2 |
| m |
| x |
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积.
考点:反比例函数与一次函数的交点问题
专题:代数几何综合题,数形结合
分析:根据两个函数的交点坐标,联立两函数的解析式,所得方程组的解即为A、B点的坐标.由于△OAB的边不在坐标轴上,因此可用其他图形面积的和差来求出△AOB的面积.
解答: 解:(1)根据题意,A点的坐标为(a,2),B点的坐标为(-4,n)
解:(1)根据题意,A点的坐标为(a,2),B点的坐标为(-4,n)
将A点的坐标(a,2)代入y=kx+
和y=
得:
得到,mk=-1 ①
将B点的坐标(-4,n) 代入y=kx+
和y=
得:n=-4k+
n=
整理得:m=16k-10 ②
将②代入 ①
得:k(16k-10)=-1
所以16k2-10k+1=0
(8k-1)(2k-1)=0
得k=
,k=
分别验证:将k=
代入①,
得m=-8所以a=-4,n=2
此时A、B坐标相同,不合题意
将k=
代入 ①,
得m=-2所以a=-1,n=
,
点A(-1,2),B(-4,
),
所以一次函数是:y=
+
反比例函数是:y=-
.
(2)分别过点A,B作x轴,y轴的垂线,交于点F,分别交x,y轴于点D、E,如图,
S矩形ODFE=4×2=8,
S△ABF=
×
×3=
,
S△OBD=
×
×4=1,
S△AOE=
×1×2=1,
S△AOB=S矩形ODFE-S△ABF-S△OBD-S△AOE=
,
所以△AOB的面积
.
 解:(1)根据题意,A点的坐标为(a,2),B点的坐标为(-4,n)
解:(1)根据题意,A点的坐标为(a,2),B点的坐标为(-4,n) 将A点的坐标(a,2)代入y=kx+
| 5 |
| 2 |
| m |
| x |
得:
|
得到,mk=-1 ①
将B点的坐标(-4,n) 代入y=kx+
| 5 |
| 2 |
| m |
| x |
得:n=-4k+
| 5 |
| 2 |
n=
| m |
| -4 |
整理得:m=16k-10 ②
将②代入 ①
得:k(16k-10)=-1
所以16k2-10k+1=0
(8k-1)(2k-1)=0
得k=
| 1 |
| 8 |
| 1 |
| 2 |
分别验证:将k=
| 1 |
| 8 |
得m=-8所以a=-4,n=2
此时A、B坐标相同,不合题意
将k=
| 1 |
| 2 |
得m=-2所以a=-1,n=
| 1 |
| 2 |
点A(-1,2),B(-4,
| 1 |
| 2 |
所以一次函数是:y=
| x |
| 2 |
| 5 |
| 2 |
反比例函数是:y=-
| 2 |
| x |
(2)分别过点A,B作x轴,y轴的垂线,交于点F,分别交x,y轴于点D、E,如图,
S矩形ODFE=4×2=8,
S△ABF=
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
S△OBD=
| 1 |
| 2 |
| 1 |
| 2 |
S△AOE=
| 1 |
| 2 |
S△AOB=S矩形ODFE-S△ABF-S△OBD-S△AOE=
| 15 |
| 4 |
所以△AOB的面积
| 15 |
| 4 |
点评:本题综合考查用待定系数法求反比例函数与一次函数的解析式.本题难度较大,利用反比例函数和一次函数的知识求三角形的面积,因为△AOB的边都不在坐标轴上,所以直接利用三角形的面积计算公式来求这个三角形的面积比较烦琐,也比较难,因此需要将这个三角形转化为两个有一边在坐标上的三角形来求面积.本题也可以利用上面的方法来求△AOB的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在直角三角形中,如果一直角边的长为2cm,斜边长为
cm,则另一直角边长是( )
| 7 |
| A、1cm | ||
B、
| ||
C、
| ||
| D、2cm |
下列变形正确的是( )
A、如果2x=5,那么x=
| ||||
| B、如果2x-3=7,那么2x=7+3 | ||||
| C、如果-3(x-2)=x+1,那么-3x-6=x+1 | ||||
D、如果
|
观察下列图形:

它们是按一定规律排列,依照此规律,第20个图形共有?( )

它们是按一定规律排列,依照此规律,第20个图形共有?( )
| A、58个 | B、60个 |
| C、62个 | D、64个 |
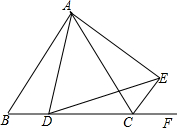 如图,△ABC为等边三角形,D为BC边上一点,以AD为边作∠ADE=60°,DE与△ABC的外角平分线CE交于点E,连结AE,试判断△ADE的形状,并说明理由.
如图,△ABC为等边三角形,D为BC边上一点,以AD为边作∠ADE=60°,DE与△ABC的外角平分线CE交于点E,连结AE,试判断△ADE的形状,并说明理由. 已知平面直角坐标系中,A(0,6),B(8,3),求满足△ABC是等腰直角三角形时点C的坐标.
已知平面直角坐标系中,A(0,6),B(8,3),求满足△ABC是等腰直角三角形时点C的坐标. 在下面的横线上填上推理的根据,
在下面的横线上填上推理的根据,