题目内容
11.若x1,x2是一元二次方程x2-3x-1=0的两根,则$\frac{1}{x_1}$+$\frac{1}{x_2}$的值是-3,x12+x22=11.分析 根据韦达定理得出x1+x2=3,x1x2=-1,再整体代入$\frac{1}{x_1}$+$\frac{1}{x_2}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$、x12+x22=(x1+x2)2-2x1x2可得答案.
解答 解:∵x1,x2是一元二次方程x2-3x-1=0的两根,
∴x1+x2=3,x1x2=-1,
则$\frac{1}{x_1}$+$\frac{1}{x_2}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=-3,
x12+x22=(x1+x2)2-2x1x2=11,
故答案为:-3,11.
点评 本题主要考查根与系数的关系,掌握x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$是关键.

练习册系列答案
相关题目
20.使$\sqrt{3x-4}$有意义的x的取值范围是( )
| A. | x>$\frac{4}{3}$ | B. | x>$\frac{3}{4}$ | C. | x$≥\frac{3}{4}$ | D. | x≥$\frac{4}{3}$ |
1.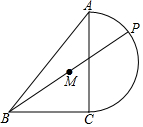 如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )
如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )
 如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )
如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )| A. | 2$\sqrt{2}$π | B. | $\sqrt{2}$π | C. | 2π | D. | 2$\sqrt{2}$ |