题目内容
19.设M=$\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+…}}}}$,N=1+$\frac{1}{1+\frac{1}{1+\frac{1}{1+…}}}$,则( )| A. | M>N | B. | M=N | ||
| C. | M<N | D. | M与N的大小关系无法确定 |
分析 运用方程的思想和M与N的特征得到M=$\sqrt{1+M}$,N=1+$\frac{1}{N}$,然后分别解方程即可判断M与N的大小关系.
解答 解:根据题意得M=$\sqrt{1+M}$,N=1+$\frac{1}{N}$,
变形得M2-M-1=0,N2-N-1=0(M>0,N>0),
解得M=$\frac{1+\sqrt{5}}{2}$,N=$\frac{1+\sqrt{5}}{2}$.
所以M=N.
故选B.
点评 本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.也考查了方程的思想.

练习册系列答案
相关题目
7.将一张面值50元的人民币,兑换成5元或10元的零钱,那么兑换方案共有( )
| A. | 5种 | B. | 6种 | C. | 7种 | D. | 8种 |
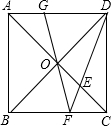 如图,O为正方形ABCD对角线的交点,E是线段OC的中点,DE的延长线交BC边于点F,连接并延长FO交AD于点G.若AB=2,则GF=$\frac{2\sqrt{10}}{3}$.
如图,O为正方形ABCD对角线的交点,E是线段OC的中点,DE的延长线交BC边于点F,连接并延长FO交AD于点G.若AB=2,则GF=$\frac{2\sqrt{10}}{3}$.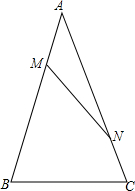 如图,已知△ABC中,AB=AC,AM=CN,探求:∠ABC与∠ANM满足∠B-∠ANM=30°时,$\frac{MN}{BC}$=$\frac{\sqrt{3}}{3}$.
如图,已知△ABC中,AB=AC,AM=CN,探求:∠ABC与∠ANM满足∠B-∠ANM=30°时,$\frac{MN}{BC}$=$\frac{\sqrt{3}}{3}$.