题目内容
17.若关于x的方程$\frac{x+1}{x+2}$-$\frac{x}{x-1}$=$\frac{ax+2}{(x-1)(x+2)}$无解,则a=-5、-2或-$\frac{1}{2}$.分析 分式方程无解的条件是:去分母后所得整式方程无解,或解这个整式方程得到的解使原方程的分母等于0.
解答 解:方程去分母得:(x-1)(x+1)-x(x+2)=ax+2,即(a+2)x+3=0
∵方程$\frac{x+1}{x+2}$-$\frac{x}{x-1}$=$\frac{ax+2}{(x-1)(x+2)}$无解,
∴x=1或x=-2,
∴当x=1时,-3=a+2,即a=-5,
当x=-2时,3=-2a+2,即a=-$\frac{1}{2}$,
另当a=-2时,方程变为3=0,不成立,所以a=-2时,方程也无解
∴a=-5、-2或-$\frac{1}{2}$时方程无解.
故答案为-5、-2或-$\frac{1}{2}$.
点评 本题考查了分式方程的解.在解方程的过程中因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根,增根是令分母等于0的值,不是原分式方程的解.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
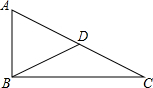 如图,Rt△ABC中∠ABC=90°,D为斜边AC的中点,AC=20cm,则BD=10cm.
如图,Rt△ABC中∠ABC=90°,D为斜边AC的中点,AC=20cm,则BD=10cm.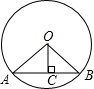 如图,AB是⊙O的弦,OC⊥AB,垂足为C,若OA=5,OC=4,则AB的长为6.
如图,AB是⊙O的弦,OC⊥AB,垂足为C,若OA=5,OC=4,则AB的长为6.
 一只蜘蛛正处于一个正方体的一个顶点A处,一只苍蝇处于此正方体的另一个顶点B处(如图所示),如果此正方体的棱长恰为10cm,试问蜘蛛想捉到苍蝇的最短路线是10$\sqrt{5}$cm.
一只蜘蛛正处于一个正方体的一个顶点A处,一只苍蝇处于此正方体的另一个顶点B处(如图所示),如果此正方体的棱长恰为10cm,试问蜘蛛想捉到苍蝇的最短路线是10$\sqrt{5}$cm.