题目内容
2.当0≤x≤1时,求函数y=x2+ax+b的最值.分析 分类讨论:当a>0时,当-$\frac{1}{4}$<a<0时,当-2<a<-$\frac{1}{4}$时,当a≤-2时,根据二次函数的增减性,可得答案.
解答 解:当a>0时,x=0时,y最小=b,x=1时y最大=a+b+1;
当-$\frac{1}{4}$<a<0时,y最小=$\frac{4b-{a}^{2}}{4}$,x=1时,y最大=a+b+1;
y最小=$\frac{4b-{a}^{2}}{4}$,x=0时,y最大=b;
当a≤-2时,y最小=a+b+1,y最大=b.
点评 本题考查了二次函数的最值,利用了二次函数的增减性,分类讨论是解题关键,以防遗漏.

练习册系列答案
相关题目
11.下列计算中错误的是( )
| A. | (-20)-(-5)=-15 | B. | 1-(+7)=-6 | C. | 0-(+2)=-2 | D. | (-5)-(+5)=0 |
11.当-1≤x≤1时,在实数范围内下列式子有意义的是( )
| A. | $\sqrt{(x+1)(x-1)}$ | B. | $\sqrt{(x+1)(1-x)}$ | C. | $\sqrt{\frac{x+1}{x-1}}$ | D. | $\sqrt{\frac{x-1}{x+1}}$ |
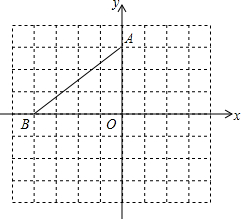 在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0)
在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0)