题目内容
12.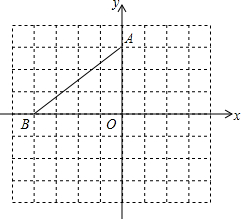 在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0)
在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0)(1)将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F,请在图中画出△AEF;
(2)将线段AF绕点O旋转180°得到线段MN,点A、F对应点分别是M、N,请画出线段MN,并连结NF,直接写出线段NF的长.
分析 (1)利用网格特点和旋转的性质画出点O,B对应点分别是E,F,即可得到△AEF;
(2)利用关于原点中心对称的点的坐标特征找出点A、F对应点分别是M、N,则可得到线段MN,然后利用勾股定理计算NF的长.
解答 解:(1)如图,△AEF为所作;
(2)如图,MN为所作,
NF=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
相关题目
3.中国人民解放军标准时间,通过北斗系统发播全军,达到了每年误差小于百万分之一秒的世界先进水平.用科学记数法表示“百万分之一”为( )
| A. | 1×106 | B. | 1×10-6 | C. | 1×102 | D. | 1×10-5 |
20.一种袋装大米的质量标准记为“10±0.3kg”,现有四袋这种大米,其中不符合标准的是( )
| 袋号 | 一 | 二 | 三 | 四 |
| 质量/kg | 9.6 | 9.7 | 9.9 | 10.2 |
| A. | 第一袋 | B. | 第二袋 | C. | 第三袋 | D. | 第四袋 |

