题目内容
如图,对称轴为直线x=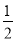 的抛物线与y轴交于点C(0,﹣3),与x轴交于A、B两点(点A在点B的左侧),AB=5
的抛物线与y轴交于点C(0,﹣3),与x轴交于A、B两点(点A在点B的左侧),AB=5
(1)求A、B两点的坐标及该抛物线对应的解析式;
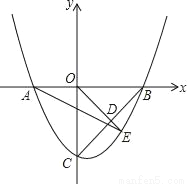
(2)D为BC的中点,延长OD与抛物线在第四象限内交于点E,连结AE、BE.
①求点E的坐标;
②判断ABE的形状,并说明理由;
(3)在x轴下方的抛物线上,是否存在一点P,使得四边形OBEP是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
练习册系列答案
相关题目
题目内容
如图,对称轴为直线x=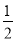 的抛物线与y轴交于点C(0,﹣3),与x轴交于A、B两点(点A在点B的左侧),AB=5
的抛物线与y轴交于点C(0,﹣3),与x轴交于A、B两点(点A在点B的左侧),AB=5
(1)求A、B两点的坐标及该抛物线对应的解析式;
(2)D为BC的中点,延长OD与抛物线在第四象限内交于点E,连结AE、BE.
①求点E的坐标;
②判断ABE的形状,并说明理由;
(3)在x轴下方的抛物线上,是否存在一点P,使得四边形OBEP是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
