题目内容
抛物线y=ax2+bx+c经过原点,其顶点坐标为(1,
),与x轴交于另一点A.
(1)求此抛物线的解析式;
(2)将直线y=
x向下平移与抛物线交于EF两点,若∠EOF=90°,求平移后的直线解析式.

| 1 |
| 3 |
(1)求此抛物线的解析式;
(2)将直线y=
| 1 |
| 2 |

考点:二次函数图象与几何变换,待定系数法求二次函数解析式
专题:
分析:(1)设顶点式y=a(x-1)2+
,然后把原点坐标代入求出a即可;
(2)设E(x1,y1),(x2,y2),利用勾股定理和两点间的距离公式得到x12+y12+x22+y22=(x2-x1)2+(y2-y1)2,整理得到x1x2+y1y2=0,再根据一次函数图象的平移问题得到直线y=
x向下平移n个单位后的解析式为y=
x+n,则根据二次函数图象与异次函数图象的交点问题得到
,消去y得-
x2+
x=
x+n,整理得2x2-x+6n=0,利用根与系数的关系得到x1+x2=
,x1x2=3n,接着用n表示y1y2,然后利用x1x2+y1y2=0得到关于n的一元二次方程,再解方程即可得到n的值.
| 1 |
| 3 |
(2)设E(x1,y1),(x2,y2),利用勾股定理和两点间的距离公式得到x12+y12+x22+y22=(x2-x1)2+(y2-y1)2,整理得到x1x2+y1y2=0,再根据一次函数图象的平移问题得到直线y=
| 1 |
| 2 |
| 1 |
| 2 |
|
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵抛物线的顶点坐标为(1,
),
∴抛物线解析式为y=a(x-1)2+
把(0,0)代入a=-
,
∴抛物线解析式为y=-
x2+
x;
(2)设E(x1,y1),(x2,y2),
∵∠EOF=90°,
∴OE2+OF2=EF2,
∴x12+y12+x22+y22=(x2-x1)2+(y2-y1)2,
∴x1x2+y1y2=0,
直线y=
x向下平移n个单位后的解析式为y=
x+n,
由方程组
得-
x2+
x=
x+n,
整理得2x2-x+6n=0,
∴x1+x2=
,x1x2=3n,
∵y1y2=(
x1+n)(
x2+n)=
x1x2+
n(x1+x2)+n2=
•3n+
n•
+n2=n2+n,
∴3n+n2+n=0,解得n1=0(舍去),n2=-4,
∴n的值为-4.
| 1 |
| 3 |
∴抛物线解析式为y=a(x-1)2+
| 1 |
| 3 |
把(0,0)代入a=-
| 1 |
| 3 |
∴抛物线解析式为y=-
| 1 |
| 3 |
| 2 |
| 3 |
(2)设E(x1,y1),(x2,y2),
∵∠EOF=90°,
∴OE2+OF2=EF2,
∴x12+y12+x22+y22=(x2-x1)2+(y2-y1)2,
∴x1x2+y1y2=0,
直线y=
| 1 |
| 2 |
| 1 |
| 2 |
由方程组
|
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
整理得2x2-x+6n=0,
∴x1+x2=
| 1 |
| 2 |
∵y1y2=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
∴3n+n2+n=0,解得n1=0(舍去),n2=-4,
∴n的值为-4.
点评:本题考查了一次函数图象与几何变换:一次函数y=kx+b向下平移m个单位所得直线解析式为y=kx+b-m.也考查了勾股定理和根与系数的关系、二次函数图象与二次函数图象的交点问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
我校一位同学从2015年元月1号开始每天记录当天的最低气温,然后绘成统计图,为了直观反应气温的变化情况,他应选择( )
| A、折线图 | B、扇形图 |
| C、条形图 | D、以上都合适 |
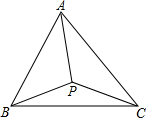 如图,△ABC内有一点P,且PA=PB=PC,若∠PAB=30°,∠PAC=40°,则∠BPC的大小是( )
如图,△ABC内有一点P,且PA=PB=PC,若∠PAB=30°,∠PAC=40°,则∠BPC的大小是( )| A、110° | B、130° |
| C、120° | D、140° |
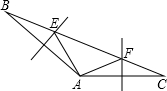 已知△ABC中,∠BAC=110°,AB、AC的垂直平分线分别交于BC于E,F,则∠EAF的度数( )
已知△ABC中,∠BAC=110°,AB、AC的垂直平分线分别交于BC于E,F,则∠EAF的度数( )| A、20° | B、40° |
| C、50° | D、60° |
 如图,Rt△ABC中,∠C=90°,AC=3,BC=4,以C点为圆心,CA为半径的圆与AB,BC分别交于点D,E,则弦AD的长为
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,以C点为圆心,CA为半径的圆与AB,BC分别交于点D,E,则弦AD的长为