题目内容
如图，已知动点A（a，b）在反比例函数y=| 4 |
| x |
| A、由小变大 | B、由大变小 |
| C、一直不变 | D、先增大后减少 |
考点：反比例函数系数k的几何意义
专题：计算题
分析：作DH⊥x轴于H，如图，根据反比例函数比例系数k的几何意义得到四边形ABOC为矩形，S矩形ABOC=ab=4，再证明Rt△OBC∽Rt△HDB，得到
=
，设DH=t，则BH=
t，得到D点坐标为（a+
t，t），根据反比例函数图象上点的坐标特征得到（a+
t）•t=4，然后利用S△BCD=S梯形DHOC-S△BOC-S△BHD进行计算得到△BCD的面积为4．
| OB |
| DH |
| OC |
| BH |
| b |
| a |
| b |
| a |
| b |
| a |
解答：解：作DH⊥x轴于H，如图，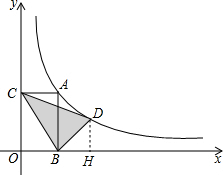
∵AB⊥x轴于点B，AC⊥y轴于点C，
∴四边形ABOC为矩形，S矩形ABOC=ab=4，
∵∠CBD=90°，
∴∠OBC+∠HBD=90°，
而∠OBC+∠BCO=90°，
∴∠BCO=∠HBD，
∴Rt△OBC∽Rt△HDB，
∴
=
，
设DH=t，则
=
，
∴BH=
t，
∴D点坐标为（a+
t，t）
∴（a+
t）•t=4，
∵S△BCD=S梯形DHOC-S△BOC-S△BHD
=
（t+b）•（a+
t）-
•t•
t
=
t•（a+
t）+
b（a+
t）-
•
t2
=
t•（a+
t）+
ab+
•
t2-
•
t2
=
×4+
×4
=4．
即△BCD的面积为定值．
故选C．
∵AB⊥x轴于点B，AC⊥y轴于点C，
∴四边形ABOC为矩形，S矩形ABOC=ab=4，
∵∠CBD=90°，
∴∠OBC+∠HBD=90°，
而∠OBC+∠BCO=90°，
∴∠BCO=∠HBD，
∴Rt△OBC∽Rt△HDB，
∴
| OB |
| DH |
| OC |
| BH |
设DH=t，则
| a |
| t |
| b |
| BH |
∴BH=
| b |
| a |
∴D点坐标为（a+
| b |
| a |
∴（a+
| b |
| a |
∵S△BCD=S梯形DHOC-S△BOC-S△BHD
=
| 1 |
| 2 |
| b |
| a |
| 1 |
| 2 |
| b |
| a |
=
| 1 |
| 2 |
| b |
| a |
| 1 |
| 2 |
| b |
| a |
| 1 |
| 2 |
| b |
| a |
=
| 1 |
| 2 |
| b |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| b |
| a |
| 1 |
| 2 |
| b |
| a |
=
| 1 |
| 2 |
| 1 |
| 2 |
=4．
即△BCD的面积为定值．
故选C．
点评：本题考查了反比例函数比例系数k的几何意义：在反比例函数y=
图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．也考查了相似三角形的判定与性质．
| k |
| x |
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
下列有关向量的等式中，不一定成立的是（ ）
A、
| ||||||||
B、|
| ||||||||
C、
| ||||||||
D、|
|