题目内容
 如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在点C′的位置,若BC=2
如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在点C′的位置,若BC=2| 3 |
考点:翻折变换(折叠问题)
专题:
分析:首先证明线段CD⊥BC且平分BC,然后求出线段CC′的长即可解决问题.
解答: 解:如图,连接CC′.
解:如图,连接CC′.
由题意得∠C′DC=2×45°=90°,
∵AD是△ABC的中线,BC=2
,
∴BD=DC=
;
∴DC′是BC的垂直平分线,
∴BC′=CC′;
∵CC′=
=
,
∴BC′=
,
故答案为:
.
 解:如图,连接CC′.
解:如图,连接CC′.由题意得∠C′DC=2×45°=90°,
∵AD是△ABC的中线,BC=2
| 3 |
∴BD=DC=
| 3 |
∴DC′是BC的垂直平分线,
∴BC′=CC′;
∵CC′=
(
|
| 6 |
∴BC′=
| 6 |
故答案为:
| 6 |
点评:该命题主要考查了几何变换中的翻折变换问题;解题的关键是灵活运用翻折变换的性质来分析、判断、推理或解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,DE∥BC,DE分别与AB、AC交于点D、E,且
如图,在△ABC中,DE∥BC,DE分别与AB、AC交于点D、E,且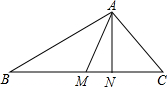 如图所示,AM为△ABC的中线,N在BC上,AB>AC,AC2•BN=AB2•CN,求证:∠BAM=∠CAN.
如图所示,AM为△ABC的中线,N在BC上,AB>AC,AC2•BN=AB2•CN,求证:∠BAM=∠CAN. 如图,已知∠AOB及点C、D两点,请利用直尺和圆规作一点P,使得点P到射线OA、OB的距离相等,且P点到点C、D的距离也相等.
如图,已知∠AOB及点C、D两点,请利用直尺和圆规作一点P,使得点P到射线OA、OB的距离相等,且P点到点C、D的距离也相等. 如图,已知反比例函数y=
如图,已知反比例函数y=