题目内容
7．已知函数y=（x-2）（x-4），当m≤x≤m+1时，求y的最小值．分析 先求出抛物线对称轴x=3，然后分m≤3，m＞3两种情况，根据二次函数的增减性解答．
解答 解：函数y=（x-2）（x-4）的对称轴是x=3，
∴当x≤3时，y随x的增大而减小，
∴m＜2，此时x=m+1时取最小值m2-4m+3；2≤m≤3时，最小值是-1；m＞3时，x=m取最小值m2-6m+8．
点评 本题考查了二次函数的最值问题，主要利用了二次函数的增减性，注意根据二次函数的对称轴分情况讨论求解．
练习册系列答案
优等生题库系列答案
相关题目
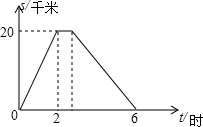在一条笔直的公路上，依次有A、C、B三地．小明从A地途经C地前往距A地20千米的B地，到B地休息一段时间后立即按原路返回到A地．小明出发4小时的时候距离A地12千米．小明去时从C地到B地，返回时再由B地到C地（包括在B地休息的时间）共用2小时．他与A地的距离s（单位：千米）和所用的时间t（单位：小时）之间的函数关系如图所示．下列说法：①小明去时的速度为10千米/时；②小明在B地休息了$\frac{2}{3}$小时；③小明回来时的速度为6千米/时；④C地与A地的距离为15千米，其中正确的个数为（ ）
如图，正方形ABCD是一块绿化带，其中阴影部分EFGH是正方形花圃．一只小鸟随机落在绿化带区域内，则它停留在花圃上的概率是$\frac{2}{9}$．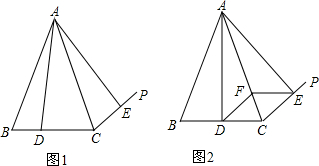
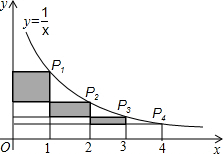在反比例函数y=$\frac{1}{x}$（x＞0）的图象上，有点P1，P2，…，P2011，…，它们的横坐标依次为1，2，…2011，…分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为S1，S2，…，S2010…，则S1+S2+…+S2010=$\frac{2010}{2011}$．
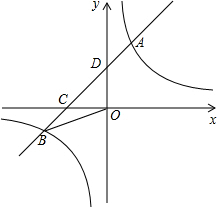如图，在平面直角坐标系中，一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的图象交于一、三象限的A、B两点，与x轴交于点C，与y轴交于点D，已知点B的坐标为（-5，-2），C为BD的中点．
16．已知5个正数a1，a2，a3，a4，a5的平均数是a，且a1＞a2＞a3＞a4＞a5，则数据a1，a2，a3，0，a4，a5的平均数和中位数是（ ）
| A． | a，$\frac{{a}_{3}}{2}$ | B． | a，$\frac{{a}_{3}+{a}_{4}}{2}$ | C． | $\frac{5}{6}$a，$\frac{{a}_{3}+{a}_{4}}{2}$ | D． | $\frac{5}{6}$a，$\frac{{a}_{3}}{2}$ |
17．“五一”节老同学聚会，每两个人都握一次手，所有人共握手28次，则参加聚会的人数是（ ）
| A． | 7 | B． | 8 | C． | 9 | D． | 10 |