Question

如图，在⊙A中，点B是弦DC，EF延长线的交点．求证：BC•BD=BF•BE．

Answer 1

考点：切割线定理

专题：证明题

分析：首先连接DE、CF，根据圆内接四边形的性质可得∠D+∠CFE=180°，∠E+∠FCD=180°，然后再证明∠D=∠BFC，∠E=∠BCF，进而可证出△BCF∽△BED，根据相似三角形的性质可得

CB

BE

=

FB

DB

，根据比例的性质进而可得结论．

解答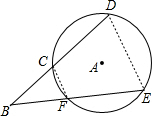：证明：连接DE、CF，
∵四边形CFED是圆内接四边形，
∴∠D+∠CFE=180°，∠E+∠FCD=180°，
∵∠BFC+∠CFE=180°，∠BCF+∠FCD=180°，
∴∠D=∠BFC，∠E=∠BCF，
∴△BCF∽△BED，
∴

CB

BE

=

FB

DB

，
∴BC•BD=BF•BE．

点评：此题主要考查了切割线定理，关键是正确证明△BCF∽△BED．