题目内容
 如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,且BE=8cm.
如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,且BE=8cm.(1)求∠D的度数;
(2)若BC=10cm,求ED的长.
考点:等边三角形的判定与性质
专题:综合题
分析:(1)延长ED交BC于点F,延长AD交BC于H,由∠EBC=∠E=60°可得△BEF是等边三角形,从而得到EF=BF=BE=8,∠EFB=60°.由AB=AC,AD平分∠BAC可得∠AHC=90°,从而可得∠HDF=30°,根据对顶角相等即可得到∠ADE=∠HDF=30°;
(2)由BC=10可得FC=2,根据等腰三角形的性质(三线合一)可得HC=5,从而可得HF=3.在Rt△DHF中,由∠HDF=30°可得DF=2HF=6,由此即可求出ED的长.
(2)由BC=10可得FC=2,根据等腰三角形的性质(三线合一)可得HC=5,从而可得HF=3.在Rt△DHF中,由∠HDF=30°可得DF=2HF=6,由此即可求出ED的长.
解答: 解:(1)延长ED交BC于点F,延长AD交BC于H,如图.
解:(1)延长ED交BC于点F,延长AD交BC于H,如图.
∵∠EBC=∠E=60°,
∴△BEF是等边三角形,
∴EF=BF=BE=8,∠EFB=60°.
∵AB=AC,AD平分∠BAC,
∴AH⊥BC,即∠AHC=90°,
∴∠HDF=30°,
∴∠ADE=∠HDF=30°;
(2)∵BC=10,
∴FC=2.
∵AB=AC,AD平分∠BAC,
∴BH=CH=
BC=5,
∴HF=5-2=3.
在Rt△DHF中,
∵∠HDF=30°,
∴DF=2HF=6,
∴DE=8-6=2.
∴ED的长为2cm.
 解:(1)延长ED交BC于点F,延长AD交BC于H,如图.
解:(1)延长ED交BC于点F,延长AD交BC于H,如图.∵∠EBC=∠E=60°,
∴△BEF是等边三角形,
∴EF=BF=BE=8,∠EFB=60°.
∵AB=AC,AD平分∠BAC,
∴AH⊥BC,即∠AHC=90°,
∴∠HDF=30°,
∴∠ADE=∠HDF=30°;
(2)∵BC=10,
∴FC=2.
∵AB=AC,AD平分∠BAC,
∴BH=CH=
| 1 |
| 2 |
∴HF=5-2=3.
在Rt△DHF中,
∵∠HDF=30°,
∴DF=2HF=6,
∴DE=8-6=2.
∴ED的长为2cm.
点评:本题主要考查了等边三角形的判定与性质、等腰三角形的性质、30°角所得的直角边等于斜边的一半等知识,由∠EBC=∠E=60°联想到构造等边三角形是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
“一个数x的2倍与3的和”用代数式可表示为( )
| A、2(x+3) |
| B、(2+x)x |
| C、2x+3 |
| D、2+3x |
 如图,在⊙A中,点B是弦DC,EF延长线的交点.求证:BC•BD=BF•BE.
如图,在⊙A中,点B是弦DC,EF延长线的交点.求证:BC•BD=BF•BE. 已知:如图,在矩形ABCD中,对角线交于点O,MN过点O分别与AD相交于点M,与BC相交于点N,且MN=2NC,MN⊥BD.
已知:如图,在矩形ABCD中,对角线交于点O,MN过点O分别与AD相交于点M,与BC相交于点N,且MN=2NC,MN⊥BD. (1)如图,AD是△ABC的中线,△ABC与△ABD的面积有怎样的数量关系?为什么?
(1)如图,AD是△ABC的中线,△ABC与△ABD的面积有怎样的数量关系?为什么?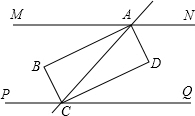 已知MN∥PQ,AB,BC分别平分∠MAC,∠PCA,交于点B,AD,DC分别平分∠NAC,∠QCA,交于点D.求证:四边形ABCD是矩形.
已知MN∥PQ,AB,BC分别平分∠MAC,∠PCA,交于点B,AD,DC分别平分∠NAC,∠QCA,交于点D.求证:四边形ABCD是矩形.