题目内容
1. 课本上有这样一道题目:
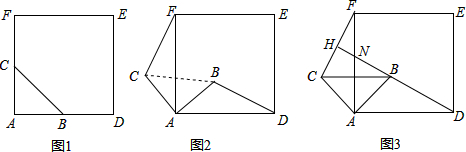
课本上有这样一道题目:如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA.
(1)求∠DAE的度数;
(2)如果把题目中“AB=AC”的条件舍去,其余条件不变,那么∠DAE的度数是否改变吗,并说明理由;
(3)如果把题目中“∠BAC=90°”的条件改为“∠BAC>90°”,其余条件不变,那么∠DAE与∠BAC有怎样的数量关系,并说明理由?
分析 (1)由于AB=AC,∠BAC=90°,从而求出∠B=∠ACB=45°,又因为BD=BA,可知∠BAD=∠BDA=67.5°,因为CE=CA,可知∠CAE=∠E=$\frac{1}{2}$∠ACB=22.5°,最后可求出得∠DAE=∠BAE-∠BAD=45°.
(2)可设∠CAE=x,从而可知∠E=x,∠ACB=2x,∠B=90°-∠ACB=90°-2x,然后可求出∠BAD=∠BDA=x+45°,∠BAE=90°+x,所以∠DAE=∠BAE-∠BAD=(90°+x)-(x+45°)=45°,
(3)可设∠CAE=x,∠BAD=y,则∠B=180°-2y,∠E=∠CAE=x,从而可知∠BAE=2y-x,∠DAE=y-x,∠BAC=2y-2x,所以可知∠DAE=$\frac{1}{2}$∠BAC,
解答 解:(1)∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵BD=BA,
∴∠BAD=∠BDA=$\frac{1}{2}$(180°-∠B)=67.5°,
∵CE=CA
∴∠CAE=∠E=$\frac{1}{2}$∠ACB=22.5°,
∴∠BAE=180°-∠B-∠E=112.5°,
∴∠DAE=∠BAE-∠BAD=45°,
(2)不改变
设∠CAE=x,则∠E=x,∠ACB=2x,
∵∠B=90°-∠ACB=90°-2x,
∴∠BAD=∠BDA=$\frac{1}{2}$(180°-∠B)=x+45°,
∠BAE=180°-∠B-∠E=90°+x,
∴∠DAE=∠BAE-∠BAD=(90°+x)-(x+45°)=45°,
(3)∠DAE=$\frac{1}{2}$∠BAC,
理由:设∠CAE=x,∠BAD=y,
则∠B=180°-2y,∠E=∠CAE=x,
∴∠BAE=180°-∠B-∠E=2y-x,
∴∠DAE=∠BAE-∠BAD=2y-x-y=y-x,
∠BAC=∠BAE-∠CAE=2y-x-x=2y-2x
∴∠DAE=$\frac{1}{2}$∠BAC,
点评 本题考查等腰三角形的性质,解题的关键是根据等腰三角形的性质分别求出各角的度数,然后利用度数计算的方法求出∠DAE与∠BAC的关系,本题属于中等题型.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案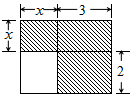 下面四个整式中,不能表示图中阴影部分面积的是( )
下面四个整式中,不能表示图中阴影部分面积的是( )| A. | (x+3)(x+2)-2x | B. | x(x+3)+6 | C. | 3(x+2)+x2 | D. | x2+5x |
| A. | y=2(x+1)2-2 | B. | y=2(x-1)2-2 | C. | y=2(x-2)2-1 | D. | y=2(x+2)2+1 |
| A. | 2cm | B. | 3cm | C. | 5cm | D. | 8cm |